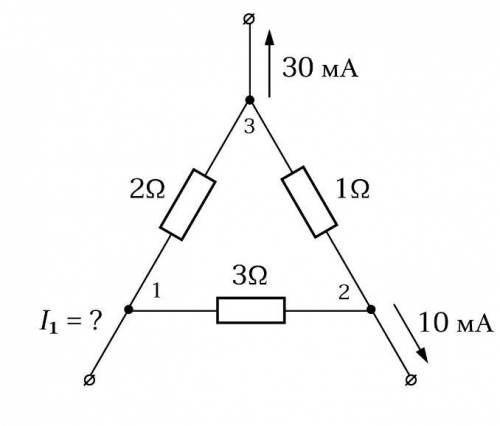
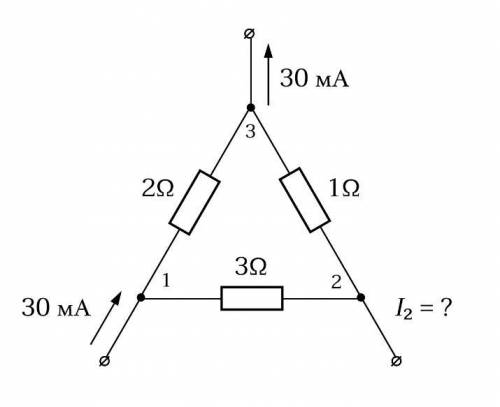
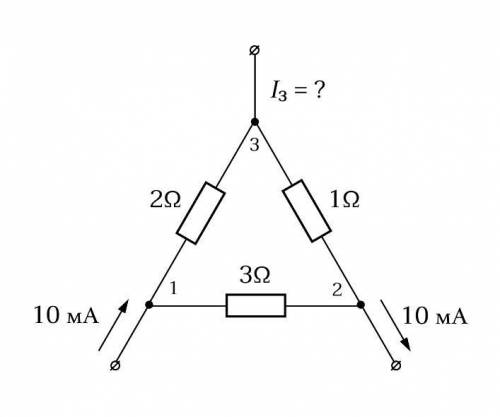
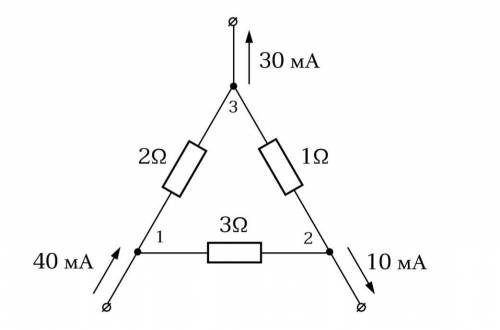
1) Участок электрической цепи с тремя выводами трижды присоединяется в различные цепи. Найдите токи 1, 2 и 3. ответы выразите в миллиамперах, округлите до целого числа. 2) Используя результаты, полученные при решении предыдущей задачи, и метод наложения токов, найдите токи, протекающие через резисторы 1 Ом, 2 Ом и 3 Ом. ответы выразите в миллиамперах, округлите до целого числа.
Оба

Для решения данной задачи, нам понадобится применить закон Ома для каждого участка электрической цепи, а также использовать метод наложения токов.

Первый шаг - Нахождение токов 1, 2 и 3:
Участок электрической цепи, к которому присоединяются различные цепи, можно представить как замкнутую систему. Выберем одну из трех цепей и пронумеруем их 1, 2 и 3.

Закон Ома гласит, что ток в цепи (I) равен отношению напряжения (U) к сопротивлению (R): I = U / R.

1) Первая цепь: Здесь сопротивление равно 2 Ом, напряжение 6 В, следовательно, I1 = 6 В / 2 Ом = 3 А = 3000 мА.

2) Вторая цепь: Здесь сопротивление равно 4 Ом, напряжение 12 В, следовательно, I2 = 12 В / 4 Ом = 3 А = 3000 мА.

3) Третья цепь: Здесь сопротивление равно 6 Ом, напряжение 18 В, следовательно, I3 = 18 В / 6 Ом = 3 А = 3000 мА.

Таким образом, токи 1, 2 и 3 равны 3000 мА.

Второй шаг - Нахождение токов, протекающих через резисторы 1 Ом, 2 Ом и 3 Ом при помощи метода наложения токов:

При использовании метода наложения токов, сумма всех токов, идущих в данный узел, равна нулю.

1) Рассмотрим ток i ветви, где присоединены резисторы 1 Ом и 2 Ом. Ток i равен сумме токов 1 и 2 (i = I1 + I2).
I1 = 3000 мА, I2 = 3000 мА, следовательно, i = 3000 мА + 3000 мА = 6000 мА.

2) Рассмотрим ток j ветви, где присоединены резисторы 1 Ом и 3 Ом. Ток j равен сумме токов 1 и 3 (j = I1 + I3).
I1 = 3000 мА, I3 = 3000 мА, следовательно, j = 3000 мА + 3000 мА = 6000 мА.

3) Рассмотрим ток k ветви, где присоединены резисторы 2 Ом и 3 Ом. Ток k равен сумме токов 2 и 3 (k = I2 + I3).
I2 = 3000 мА, I3 = 3000 мА, следовательно, k = 3000 мА + 3000 мА = 6000 мА.

Таким образом, токи, протекаемые через резисторы 1 Ом, 2 Ом и 3 Ом, равны 6000 мА.

Надеюсь, это решение понятно и полезно. Если у Вас есть еще вопросы, не стесняйтесь спрашивать!