. 1. Рассмотрите динамометры, изображенные на рисунке 80. Определите цену деления каждого динамометра и вес каждого груза. Изобразите на рисунке в тетради вес каждого груза. Укажите точку его приложения, масштаб выберите самостоятельно.
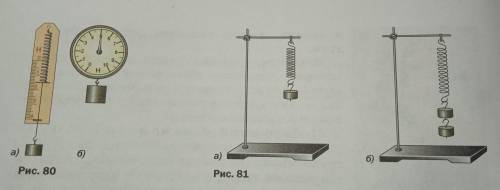
2. По рисунку 81 определите, чему равна сила, действующая на нижний конец пружины (масса одного груза 100 г). Сравните деформации пружины в случаях a и b.
3. В быту часто используются пружинные весы. Возьмитесь за петельку одной рукой, за крючок — другой и потяните. Следите за показанием стрелки. Можно ли эти весы использовать в качестве динамометра?

England is the largest and richest country in the UK. The official language of England is English, while German is also spoken. More than 48 million people live in England.The flag of England consists of two colors-white and red. The largest cities in England: London, York, Manchester, Birmingham.But the Capital of England is London.д

1. Для определения цены деления каждого динамометра и веса каждого груза, рассмотрим рисунок 80. На рисунке показаны два динамометра, каждый из которых имеет разные шкалы.

Для определения цены деления динамометра, нужно посмотреть на расположение делений на его шкале. На рисунке 80A шкала разделена на 10 равных делений, поэтому цена деления этого динамометра равна 1/10 усилия, которым тянется пружина. На рисунке 80B шкала разделена на 20 равных делений, поэтому цена деления этого динамометра равна 1/20 усилия.

Чтобы определить вес каждого груза, нужно рассмотреть максимальное удлинение пружины под действием груза и использовать закон Гука. Закон Гука гласит, что удлинение пружины прямо пропорционально приложенной к ней силе. Данный закон может быть представлен следующей формулой: F = k * x, где F - сила, k - коэффициент упругости пружины (константа), x - удлинение пружины.

На рисунке 80A можно видеть, что максимальное удлинение пружины составляет 1,5 делений на шкале. Для определения веса первого груза, нужно использовать цену деления, которую мы определили ранее. Пусть цена деления равна 1/10 усилия, тогда вес первого груза будет равен 1/10 * 1,5 = 0,15 усилия.

На рисунке 80B максимальное удлинение пружины составляет 3 деления на шкале. Вес второго груза можно определить с помощью цены деления, которую мы также определили ранее. В данном случае цена деления равна 1/20 усилия, поэтому вес второго груза будет равен 1/20 * 3 = 0,15 усилия.

Поскольку вес первого и вес второго груза равны 0,15 усилия, значит их массы также будут равны друг другу.

2. Для определения силы, действующей на нижний конец пружины на рисунке 81, нам дана масса одного груза - 100 г. Мы также должны сравнить деформации пружины в случаях a и b.

Используем снова закон Гука для определения силы. Предположим, что константа упругости пружины равна k.

В случае a деформация пружины составляет 1 деление на шкале, поэтому здесь удлинение пружины равно 1 * цена деления.

В случае b деформация пружины составляет 2 деления на шкале, поэтому удлинение пружины равно 2 * цена деления.

Сила, действующая на пружину, может быть определена, зная закон Гука: F = k * x.

Следовательно, в случае a сила, действующая на пружину, будет равна F_a = k * (1 * цена деления), а в случае b - F_b = k * (2 * цена деления).

Так как мы можем сравнить деформации пружины, то сравнение сил можно произвести также, сравнив удлинения пружины: x_a = 1 * цена деления и x_b = 2 * цена деления.

Отношение сил F_a и F_b может быть определено по отношению удлинений пружины: F_a / F_b = k * (1 * цена деления) / k * (2 * цена деления) = (1 * цена деления) / (2 * цена деления) = 1/2 = 0,5.

Таким образом, сила, действующая на пружину в случае b, в два раза больше силы, действующей на пружину в случае a.

3. В быту пружинные весы могут часто использоваться. Чтобы проверить, могут ли они использоваться в качестве динамометра, мы можем произвести определенный эксперимент.

Возьмемся за петельку одной рукой и за крючок другой, а затем потянем. При этом мы будем следить за показанием стрелки. Если показания на стрелке увеличиваются пропорционально с силой, которую мы прикладываем, тогда пружинные весы можно использовать в качестве динамометра.

Однако, есть несколько факторов, которые могут повлиять на точность показаний пружинных весов. Например, их эксплуатационные характеристики могут изменяться со временем, шкала может быть нелинейной или цена деления не постоянна. Кроме того, другие факторы, такие как трение или внешние силы, могут оказывать влияние на показания пружинных весов.

Поэтому, хотя пружинные весы могут быть хорошим инструментом для приближенного измерения силы, они не всегда могут гарантировать высокую точность и незаменимость, особенно в научных или точных измерениях.