1.если кинетическая энергия частицы wк = 0,5mc² , то модуль ее скорости равен 2.модуль скорости движения частицы, при котором кинетическая энергия частицы равна ее энергии покоя,
Другие вопросы по теме Физика
Популярные вопросы
- 1908Семейдегі 5 сыныптық орыс гимназиясына оқуға түседіТаимент мемо?...
1 - Ажал,қонақ,несібенің ғайыпқа жату себебі неде? ...
1 - Білімді ұрпақ -іргелі елдің кепілі Бұл тақырыпқа байланысты кітаптағы...
3 - В ходе исследования студент делает выводы в разной форме ...
3 - ; три метил пропан ; два этил гексан ; два , три диметил гексан...
2 - Найти деректі зат есім вот текст...
1 - 2-тапсырма. Жырдан үзінді алып, оны өңдеп, ойды жалғастырып, хат жазу....
3 - Причастный оборот. Выполни разбор предложения по образцу. Проблема...
2 - Звичаї і порядки ліліпутії: імператор, кар єра, нагороди, політичні...
2 - Товпчик з префіксом пре-(10 слів), другий стовпчик з префіксом при-(10...
2
ответ: 1.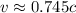 либо же
либо же 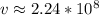 м/с
м/с
2.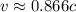 либо же
либо же 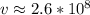 м/с
м/с
Объяснение:
1. Дано:
-----------------------------------
Т.к. из условия задачи понятно, что итоговая скорость , будет сопоставима со скоростью распространения электромагнитного излучения вакууме, то пользоваться классической механикой мы не будем, а перейдем на СТО и ЗСЭ
, будет сопоставима со скоростью распространения электромагнитного излучения вакууме, то пользоваться классической механикой мы не будем, а перейдем на СТО и ЗСЭ
Согласно ЗСЭ
Где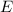 - полная энергия тела; Согласно СТО
- полная энергия тела; Согласно СТО 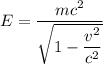
Отсюда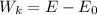
Согласно условию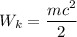
Тогда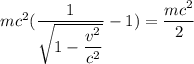 ⇒
⇒ 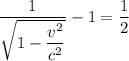 ⇒
⇒ 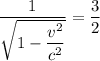 ⇒
⇒ 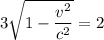 ⇒
⇒ 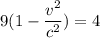 ⇒
⇒ 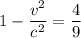 ⇒
⇒ 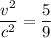 ⇒
⇒ 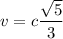
Отсюда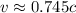 либо же
либо же 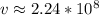 м/с
м/с
2. Дано:
----------------
В задаче 1. мы уже вывели формулу кинетической энергии тела в том случае если у нас скорость тела сопоставима со скоростью распространения электромагнитного излучения вакууме.
сопоставима со скоростью распространения электромагнитного излучения вакууме.
Согласно условию задачи 2.
(названия переменных остались такими же как и в задаче)
Тогда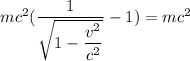 ⇒
⇒ 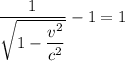 ⇒
⇒ 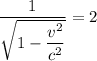 ⇒
⇒ 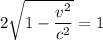 ⇒
⇒ 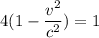 ⇒
⇒ 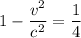 ⇒
⇒ 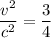 ⇒
⇒ 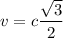
Отсюда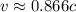 либо же
либо же 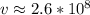 м/с
м/с