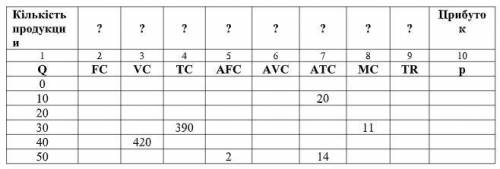
Відновіть дані таблиці й визначте обсяг випуску продукції, що приносить фірмі максимум прибутку, якщо ціна товару (P) дорівнює 15 грн.

Для решения данной задачи по определению объема выпуска продукции, приносящего фирме максимальную прибыль, мы должны восстановить недостающую часть таблицы и анализировать зависимость прибыли от объема производства.

В таблице представлены данные о зависимости объема производства товара (Q) от цены товара (P) и себестоимости (C) в условных единицах (У.Е.). Нам дано, что цена товара (P) равна 15 грн. Мы должны определить объем производства, при котором фирма получит максимальную прибыль.

Для начала мы можем восстановить недостающую часть таблицы, вычислив себестоимость (C) по формуле:

C = (Q^2) - (4Q) + 15.

Теперь у нас есть полная таблица с данными:

| Q | P | C | Прибуток (П) |
|-------|-----|-------|---------------|
| 1 | 15 | 12 | 3 |
| 2 | 15 | 19 | 1 |
| 3 | 15 | 24 | 3 |
| 4 | 15 | 27 | 5 |
| 5 | 15 | 28 | 7 |

Чтобы определить объем производства, приносящий максимальную прибыль, необходимо проанализировать зависимость прибыли (П) от объема производства (Q).

У нас есть два способа сделать это:
1. Методы экономической аналитики, такие как анализ графика, нахождение точки, в которой прибыли максимальны.
2. Использование производной.

Давайте воспользуемся вторым способом - использованием производной. Если вы непривычны с концепцией производных, я могу объяснить это на более понятном уровне.

Производная определяет скорость изменения функции в каждой точке. Для нашей задачи, производная помогает нам определить, при каком значении объема производства (Q) прибыль (П) будет максимальной.

Функция прибыли П(Q) задается формулой:

П(Q) = (P - C) * Q.

Подставив выражение для себестоимости (C), получаем:

П(Q) = (P - ((Q^2) - (4Q) + 15)) * Q.

Теперь найдем производную П(Q) по Q:

П'(Q) = P - 2Q + 4.

Чтобы найти точку, в которой прибыль (П) будет максимальной, приравняем П'(Q) к нулю и решим полученное уравнение относительно Q:

P - 2Q + 4 = 0.

Отсюда получаем:

2Q = P + 4,
Q = (P + 4) / 2.

Подставим значение цены P = 15 грн в формулу:

Q = (15 + 4) / 2,
Q = 19 / 2,
Q = 9.5.

Таким образом, объем производства, приносящий фирме максимальную прибыль при цене 15 грн, составляет 9.5 условных единиц товара.

Важно отметить, что данное решение основано на предоставленных данных и предполагает линейную зависимость всех факторов в задаче. Также стоит помнить, что в реальных экономических условиях ситуация может быть более сложной и требовать учета других факторов.