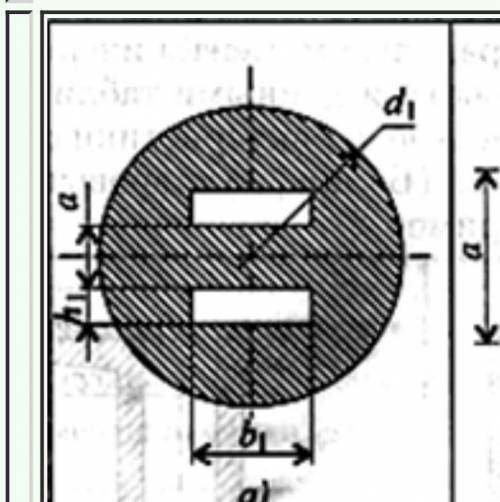
Вычислить главные центральные моменты инерции сечений, представленных на схеме. d1=72,h1=16,b1=32,a=48
Другие вопросы по теме Другие предметы
Популярные вопросы
- Выпишите подлежащие и сказуемые когда чичиков взглянул искоса на собакевича, он...
1 - Напишите небольшое сообщение на тему: мнение дворян о смутном времени ....
3 - Подобрать пословицу к легенде удзячнасть...
1 - Выполни деление с остаток в столбик и сделайте проверку: 612: 7, 792: 6, 847:...
3 - Напиши слова 2 столбика 1 слова звукавым оканчяние 2 нулевым оканчяние...
1 - Напишите описание своей комнаты на языке (не обязательно именно своей можете придумать)...
3 - Решить на скорость, время и расстояние: 1. велосипедист проехал за 4 часа 48 км,...
3 - Сочинение разважанне на тему каб крануть да слез сам зарыдае паэт....
3 - На свете существует большое количество профессий. каждая профессия интересна и...
3 - Почему женщины в церкви носят плотки а мужчины снемают галовной убор краткий ответ...
3
Для сечения 1, которое является кругом, главный центральный момент инерции вычисляется по формуле: I1 = π * (d1^4) / 64, где d1 - диаметр круга.
Подставим значения и вычислим: I1 = π * (72^4) / 64 = π * 331776 / 64 = 16368π.
Для сечения 2, которое является прямоугольником, главный центральный момент инерции вычисляется по формуле: I2 = (b2 * h2^3) / 12, где b2 - ширина прямоугольника, h2 - высота прямоугольника.
Однако, в данной схеме, нам не даны значения для ширины и высоты прямоугольника. Поэтому, мы не можем вычислить главный центральный момент инерции для сечения 2.
Для сечения 3, которое является треугольником, главный центральный момент инерции вычисляется по формуле: I3 = (b3 * h3^3) / 36, где b3 - основание треугольника, h3 - высота треугольника.
Подставим значения и вычислим: I3 = (48 * 16^3) / 36 = (48 * 4096) / 36 = 546133.33.
Итак, главные центральные моменты инерции сечений на данной схеме равны:
I1 = 16368π
I3 = 546133.33.