1. Другие предметы
  2. Вася подтянулся 12 раз, а

Вася подтянулся 12 раз, а Игорь — в 2 раза меньше. Сколько раз подтянулся Игорь?

antonishyna1997 antonishyna1997    2   17.04.2019 00:50    3

Ответы
Diana102004 Diana102004  31.05.2020 13:11

Призма прямая => объем (V) равен высота на площадь основания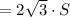 = 2\sqrt{3} \cdot S, где S - площадь основания.

 

S основания можно посчитать по формуле площади равнобедренного треугольника:

S=\frac{b\cdot\sqrt{a^2-\frac{b^2}{4}}}{2},

где a - боковая сторона, а b - основание =>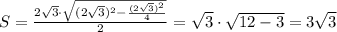 S=\frac{2\sqrt{3}\cdot\sqrt{(2\sqrt{3})^2-\frac{(2\sqrt{3})^2}{4}}}{2}=\sqrt{3}\cdot\sqrt{12-3}=3\sqrt{3}

 

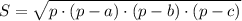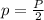Либо по формуле Герона: S=\sqrt{p\cdot(p-a)\cdot(p-b)\cdot(p-c)}, где a,b,c - стороны треугольника, а p=\frac{P}{2},

где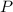 P - периметр.

 

Т.е.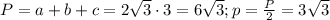 P=a+b+c=2\sqrt{3}\cdot3=6\sqrt{3}; p=\frac{P}{2}=3\sqrt{3}

 

p-a=p-b=p-c=3\sqrt{3}-2\sqrt{3}=\sqrt{3}

 

Т.о. по формуле Герона: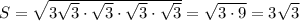 S=\sqrt{3\sqrt{3}\cdot{\sqrt{3}}\cdot{\sqrt{3}}\cdot{\sqrt{3}}}=\sqrt{3\cdot9}=3\sqrt{3}

 

Ну и объём будет:

V=h\cdot S=2\sqrt{3}\cdot3\sqrt{3}=6\cdot3=18

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Другие предметы
kiranovm14 kiranovm14  23.09.2020 06:34
Запиши два ответа о том что знаем о природных явлений на жизнь человека​...
Диана090980 Диана090980  23.09.2020 06:34
Підбрати з історії 2 позитивні якості украінців і 2 негативних якості​...
observatorshkip06tpd observatorshkip06tpd  23.09.2020 06:37
Юстиананның мемлекеттің елшілер​...
Мганвплмппррнвпол Мганвплмппррнвпол  23.09.2020 06:49
A) 5 ES; e) {2; 9} = {21; 9}; b) 18 ES; f) {21; 1} = {21; 9; 1);c) {21; 9) ES; g) 9 ES;d) {21; 9} S; h) {1; 18} - S?​...
zhludovaanasta zhludovaanasta  23.09.2020 06:50
Что такое букашка кратно ответьте мне по родному нужно...
ermekbaevadinara ermekbaevadinara  23.09.2020 06:50
Нужна ваша мне Күп нөктәләр урынына мәғәнәләре буйынса тап килгән түбәндәге мөнәсәбәт һүҙҙәрҙе өҫтәп, кәрәкле тыныш билдәләрен ҡуйып, һөйләмдәрҙә күсереп яҙығыҙ, уларҙы рус теленә...
Абдулjazair Абдулjazair  23.09.2020 06:50
Ер ТұҢға жыры қандай жыр ответте...
popovat496 popovat496  15.12.2020 17:14
Решить задачи по основам вариационного исчисления....
легенда19 легенда19  15.12.2020 17:14
Что такое любовь сочинение коротко​...
Victoriya1234567890 Victoriya1234567890  15.12.2020 17:15
ВОПРОСЫ ПО ОТИ(Основы теории информации) 1) Что такое жизненный цикл ПО ИС? 2) Перечислить вс процессы ЖЦ? 3) С какими проблемами связано обеспечение качества проекта? 4) Что относят...

Популярные вопросы