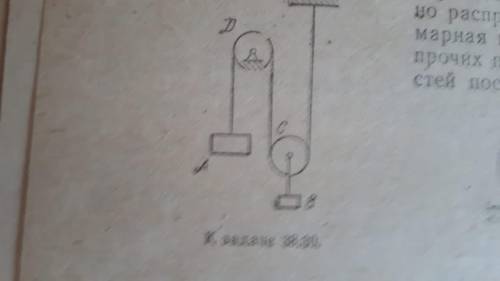
ТЕОРЕТИЧЕСКАЯ МЕХАНИКА груз а массы м1 опускаясь вниз при троса перекинутого через неподвижный блок д1, поднимает вверх груз в массы м2, прикрепленный к оси подвижного блока с и д считать однородными сплошными дисками массы м3 каждый. определить скорость груза А в момент, когда он опустится на выосту h. Масса тросса, проскальзыванием по ободам блоков и силами сопротивления принебречь. В начальный момент система находилась в покое

Добрый день!

Для решения данной задачи мы будем использовать законы сохранения энергии.

Перед тем, как начать решение, давайте ознакомимся с данными задачи:

- масса груза А равна м1
- масса груза В равна м2
- масса неподвижного блока Д равна м3
- масса подвижного блока С равна также м3
- все блоки считаем однородными сплошными дисками массой м3 каждый
- высота, на которой груз А опустится, равна h

Теперь можно приступить к решению.

1. В начальный момент система находится в покое, поэтому сумма всех внешних сил, действующих на систему, равна нулю.
2. Обозначим акселерацию груза А через а.
3. Воспользуемся первым законом Ньютона для груза А, который опускается вниз:
m1 * g - T = m1 * a (уравнение (1))
где g - ускорение свободного падения, T - сила натяжения троса, a - акселерация груза А

При этом сила натяжения троса T можно определить как:
T = (m1 + m3) * g (уравнение (2))
т.е. сумма масс груза А и блока Д, умноженная на ускорение свободного падения.

4. Также, воспользуемся вторым законом Ньютона для груза В, который поднимается:
T - m2 * g = m2 * a (уравнение (3))
При этом сила натяжения троса T здесь уже вычитается из силы тяжести груза В.

5. Поскольку система помещена в покое, грузу А приходится преодолеть высоту h.
Используем формулу для вычисления работы, которую выполняет сила F для преодоления определенного пути h:
Работа = сила * путь
В данном случае сила F - это сила натяжения троса (T), а путь h.
Также, работа равна изменению кинетической энергии системы:
Работа = ΔКЭ
m1 * g * h = (1/2) * (m1 * v^2 + m2 * v^2) (уравнение (4))
где v - скорость груза А в момент, когда он опустится на высоту h.

Будем решать систему уравнений (1), (2), (3) и (4). Обратите внимание, что уравнение (2) неизвестное T определяет через m1, m3 и g, а уравнение (3) зависит от T и m2.

Итак, для решения системы уравнений:
1. Исходя из уравнения (2), получим значение силы натяжения троса T:
T = (m1 + m3) * g.

2. Подставим это значение T в уравнение (3) и решим его относительно a:
(m1 + m3) * g - m2 * g = m2 * a
a = ((m1 + m3) - m2) * g / m2

3. Теперь, зная значение a, можем подставить его в уравнение (1) и решить его относительно T:
T = m1 * g - m1 * a

4. Наконец, получим значение скорости v подстановкой найденного значения T в уравнение (4):
m1 * g * h = (1/2) * (m1 * v^2 + m2 * v^2)
v = sqrt(2 * m1 * g * h / (m1 + m2)).

Таким образом, мы получили выражение для скорости груза А в момент, когда он опустится на высоту h.

Обратите внимание, что в данном решении мы пренебрегаем силами сопротивления, проскальзыванием троса и силами трения в блоках. Если бы это было учтено, то решение могло бы усложниться и потребовать более детального анализа.