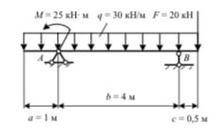
Техническая механика. Построить эпюры Q и M для нагруженной балки. Дано:

M = 25кНм

q = 30кН/м

F = 20кН

a = 1м

b = 4м

c = 0,5м

Найти: Q и Ми(Изгибающий момент)

Добрый день! Давайте рассмотрим построение эпюр Q и M для данной нагруженной балки по шагам.

Шаг 1: Рассчитаем опорную реакцию в точке A.
Сумма моментов относительно точки A равна нулю:
Mₐ - Q₁⋅a = 0,
где Mₐ - изгибающий момент в точке A, Q₁ - реакция в точке A, a - расстояние от точки A до точки B.

Из уравнения получаем, что Q₁ = Mₐ / a.

Шаг 2: Построим эпюру Q.
На рисунке отметим ось, которая будет показывать положение точек на балке. Начнем с опоры А. В точке А будет вертикальная сила Q₁. Далее, сила Q₂ на балку увеличится на q⋅c, так как мы умножаем выпуклость на длину, что дает нам силу. Затем, на b - c, между силами Q₂ и F, у нас будет горизонтальная сила F, затем на конце балки будет вертикальная сила Q₃.
Это и будет наш эпюра Q.

Шаг 3: Рассчитаем изгибающий момент Mₐ в точке A.
Сумма моментов относительно точки A равна нулю:
Mₐ - Q₁⋅a + Q₂⋅(b - a) - F⋅(b - c) = 0.

Из этого уравнения находим Mₐ:
Mₐ = Q₁⋅a - Q₂⋅(b - a) + F⋅(b - c).

Шаг 4: Построим эпюру M.
На рисунке отметим ось, которая будет показывать положение точек на балке. Начнем с опоры А. В точке А будет изгибающий момент Mₐ. Далее, изгибающий момент будет линейно увеличиваться со скоростью Q₂ в интервале от a до b. Затем, изгибающий момент будет уменьшаться со скоростью F в интервале от b до c, что соответствует сигма. В конце балки будет изгибающий момент М₃ со скоростью Q₃.
Это и будет наш эпюра M.

Шаг 5: Подставим данные в уравнения и рассчитаем Q и Mₐ.
Из уравнения Q₁ = Mₐ / a имеем:
Q₁ = 25 кНм / 1 м = 25 кН.

Из уравнения Mₐ = Q₁⋅a - Q₂⋅(b - a) + F⋅(b - c) имеем:
25 кНм = (25 кН)⋅(1 м) - Q₂⋅(4 м - 1 м) + (20 кН)⋅(4 м - 0.5 м).

Рассчитаем каждый член уравнения:
25 кНм = 25 кНм - Q₂⋅3 м + 70 кНм,

Переносим все в одну сторону:
Q₂⋅3 м = 70 кНм,

Делим на 3 м:
Q₂ = 70 кНм / 3 м ≈ 23.33 кН.

Таким образом, Q = Q₁ + Q₂ + Q₃ = 25 кН + 23.33 кН + 20 кН = 68.33 кН.

Из этих значений можно построить эпюры Q и M на балке.

Надеюсь, ответ был понятен и полезен. Если у вас возникнут дополнительные вопросы, не стесняйтесь задавать их!