Техническая механика
9 вариант

Добрый день! Я с удовольствием помогу вам разобраться с задачей по технической механике.

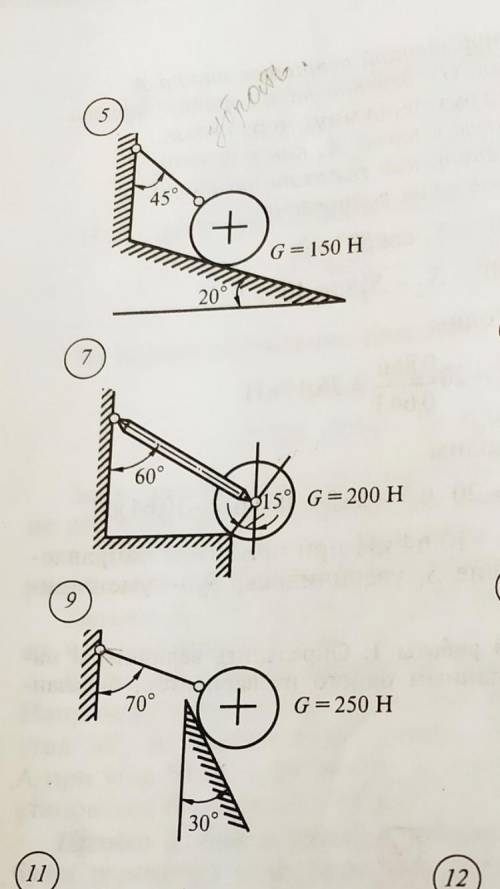
На картинке видно, что у нас есть система, состоящая из двух тел, связанных между собой нитями и находящихся на двух наклонных плоскостях.

Чтобы решить задачу, нам необходимо определить силы, действующие на каждое из тел, а также направление их действия.

Для начала, обратимся к первому телу, которое находится на наклонной плоскости. Учитывая, что тело находится в состоянии покоя, мы можем сказать, что сумма всех сил, действующих на него, равна нулю.

Первая сила, которую мы рассмотрим, это сила тяжести (F_т), которая действует вертикально вниз. Сила тяжести можно выразить через массу тела и значение ускорения свободного падения. Так как ускорение свободного падения равно примерно 9,8 м/с^2, а массу тела (m_т) необходимо найти, можно воспользоваться формулой:

F_т = m_т * g,

где F_т - сила тяжести тела,
m_т - масса тела,
g - ускорение свободного падения.

Зная, что сила тяжести направлена вниз, мы можем предположить, что наше тело поддерживается другой силой, направленной вверх. Давайте обозначим эту силу как F_оп.

Теперь обратимся ко второму телу, которое находится на другой наклонной плоскости. Как и в предыдущем случае, сумма всех сил, действующих на это тело, равна нулю.

Опять же, у нас есть сила тяжести (F_т), направленная вниз, и какая-то другая сила, направленная вверх. Давайте обозначим эту силу как F_оп2.

Теперь самое интересное. Мы знаем, что в нашей системе тела связаны нитями. Это значит, что нити развивают некоторое усилие (силы натяжения) для поддержания тел в равновесии.

Теперь давайте взглянем на картинку еще раз и рассмотрим направления и значимость всех сил:

1. Сила тяжести (F_т) для первого тела направлена вертикально вниз.
2. Сила тяжести (F_т) для второго тела также направлена вертикально вниз.
3. Сила натяжения нити (F_оп) на первом теле направлена вверх и направлена вдоль наклонной плоскости.
4. Сила натяжения нити (F_оп2) на втором теле направлена вверх и направлена вдоль наклонной плоскости.
5. Еще одна сила, действующая на первое тело, это сила трения (F_тр), которая направлена вдоль наклонной плоскости в направлении, противоположном движению. Сила трения тем важна, что она препятствует скольжению тела вниз по плоскости. Наша задача - найти ее значение.

Теперь, учитывая все силы в системе тел, мы можем записать уравнения равновесия для каждого тела:

1) F_т + F_оп + F_тр = 0,
2) F_т + F_оп2 = 0.

Теперь давайте разберемся со значениями каждой из этих сил.

Мы уже знаем, что сила тяжести (F_т) для обоих тел направлена вертикально вниз и рассчитывается по формуле F_т = m_т * g.

Теперь, чтобы рассчитать силу натяжения нити (F_оп), мы можем использовать геометрические свойства треугольника синусов. Давайте обозначим угол наклона первой плоскости как альфа. Зная, что в треугольнике синусы равны отношению противолежащего катета к гипотенузе, мы можем записать:

sin(альфа) = F_оп / F_т.

Поэтому F_оп = F_т * sin(альфа).

Точно так же, мы можем рассчитать силу натяжения нити (F_оп2) для второго тела, учитывая угол наклона второй плоскости.

Теперь осталось найти силу трения (F_тр). Для этого воспользуемся формулой, связывающей силу трения со силой нормального давления и коэффициентом трения. Пусть эта сила нормального давления обозначается как N. Тогда

F_тр = μ * N,

где μ - коэффициент трения.

В нашем случае, сила нормального давления равна проекции силы тяжести, действующей перпендикулярно плоскости. Поскольку плоскость наклонена на угол альфа, сила нормального давления (N) может быть рассчитана как:

N = F_т * cos(альфа).

Теперь мы можем найти силу трения с помощью коэффициента трения (μ) и найденного значения силы нормального давления (N).

Когда мы установим все значения сил, мы сможем подставить их в уравнения равновесия для каждого тела и решить систему уравнений.

Хочу обратить ваше внимание на то, что в данном случае я дал лишь общую методику решения задач по технической механике. Для получения конкретных результатов, необходимо знать данные и значения масс и углов наклона плоскостей.