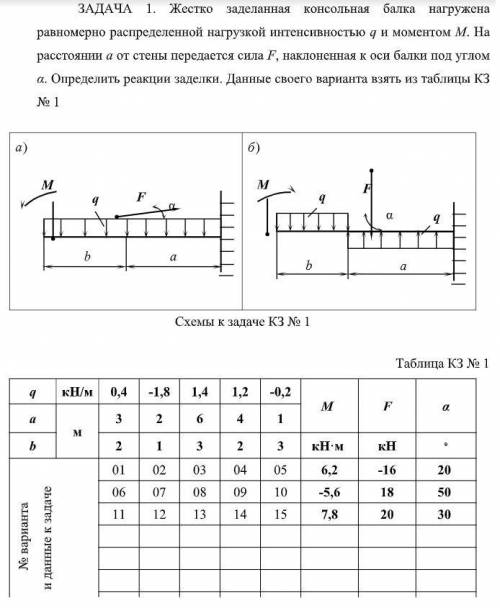
решить , завтра уже сдача ЗАДАЧА 1. Жестко заделанная консольная балка нагружена

равномерно распределенной нагрузкой интенсивностью q и моментом М. На

расстоянии а от стены передается сила F, наклоненная к оси балки под углом

α. Определить реакции заделки. Данные своего варианта взять из таблицы КЗ

Для решения этой задачи, нам нужно использовать уравнение равновесия моментов и уравнения равновесия сил.

1. Начнем с уравнения равновесия моментов. Положительные моменты считаем против часовой стрелки, а отрицательные - по часовой стрелке. Соответственно, мы можем записать уравнение равновесия моментов вокруг заделки:

М - F * a * sin(α) = 0

где М - момент нагрузки, F - сила, а - расстояние от стены до точки приложения силы F, α - угол наклона силы F к оси балки.

2. Теперь рассмотрим уравнения равновесия сил. Горизонтальные и вертикальные силы должны быть равны нулю. Мы можем записать уравнения равновесия сил вдоль оси X и оси Y:

∑F_x = 0
∑F_y = 0

3. Рассмотрим горизонтальные силы. Единственной горизонтальной силой в данной задаче является сила F, поэтому мы можем записать уравнение равновесия сил вдоль оси X:

F * cos(α) - R1 = 0

где R1 - горизонтальная реакция в точке заделки.

4. Рассмотрим вертикальные силы. В задаче указано, что балка нагружена равномерно распределенной нагрузкой, поэтому мы можем записать уравнение равновесия сил вдоль оси Y:

R2 - q * L - F * sin(α) = 0

где R2 - вертикальная реакция в точке заделки, q - интенсивность равномерно распределенной нагрузки, L - длина балки.

5. Наконец, рассмотрим момент нагрузки. Мы можем записать уравнение равновесия моментов для равномерно распределенной нагрузки:

M + q * L^2 / 2 - F * a * cos(α) = 0

Теперь мы можем использовать полученные уравнения, чтобы найти реакции заделки R1 и R2. Для этого мы должны знать значения интенсивности нагрузки q и момента нагрузки М, а также значения расстояния а и угла наклона α.

Подставим полученные значения в уравнения и решим их, чтобы найти реакции заделки R1 и R2.