При формировании женских половых клеток в отличие от мужских
Ответы
ДЛя сведения cos(-a)=cos a; sin(-a)=-sina; cos(2pi+-a)= cosa; cos(-2,8pi)=cos(2,8pi)=cos(0,8pi); sin(-2,8pi)=-sin(2,8pi)=-sin(0,8pi); sin(-4,3pi)=-sin(4,3pi)=sin0,3pi. Опираясь на все это, перепишем выражение в следующем виде: (sin0,3pi*cos0,8pi-cos0,3pi*sin0,8pi)/cos0,3pi*cos0,3pi+sin0,3pi*sin0,3pi)= sin(0,3pi-0,8pi)/cos(0,3pi)^2+sin(0,3)^2)=sin(-0,5pi)/1=-sin(0,5pi)=-1*1=-1. В числителе синус суммы, в знаменателе основное тригонометрическое тождество дает единицу.
ПОКАЗАТЬ ОТВЕТЫ
Дробь равна
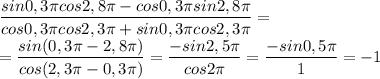
ПОКАЗАТЬ ОТВЕТЫ
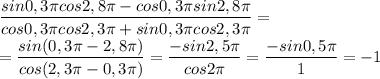
Другие вопросы по теме Другие предметы
Популярные вопросы
- Серый день короче ночи надо поставить ударение...
1 - Выберите верные суждения о функциях как науки и запишите цифры под которыми...
3 - Сколько грамм осадка выделится при взаимодействии 27,0 хлорида меди 2 с...
1 - Люди, , ! краткое содержание по рассказу л. н. толстого кавказские пленники...
2 - Решите 2 номер начиная с 3 примера, (и желательно как оформить правильно)...
1 - Сувеличением порядкового (атомного) номера электронов в периоде происходит:...
3 - 1. у котрому рядку допущено помилку при подвоєнні приголосних: а)передмістя,...
3 - Составить уравнение с неизвестным уменьшаемым так, чтобы значение неизвестного...
1 - Объем продаж в магазинке в час пик составляет 25 000р. , а в другие часы...
3 - Аральское мореа) одна часть солёная,другая пресная; б)самое крупное озеро;...
1