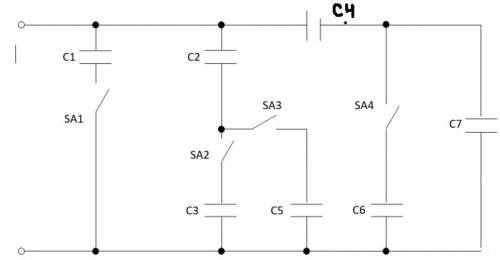
Предмет - Электроника и электротехника Определить Эквивалентную емкость Цепи (Cэкв) со смешанными соединениями конденсаторов при условии ,что емкость конденсаторов соответственно равны:
С1=2 мкФ
С2=С3=С4=С6=1 мкФ
С5 = 3 мкФ
С7= 0,5 мкФ
Если: SA2 и SA4 замкнуты SA1 и SA3 разомкнуты

Для решения данной задачи на определение эквивалентной емкости цепи с смешанными соединениями конденсаторов, нам необходимо разобраться в принципах соединения конденсаторов. Давайте начнем с базовых понятий.

Существует два типа соединения конденсаторов:
1. Параллельное соединение, когда положительные пластины конденсаторов соединяются между собой, а отрицательные пластины также соединяются между собой. В данном случае, заряды на пластинах конденсаторов складываются, а емкости конденсаторов складываются алгебраически.
2. Последовательное соединение, когда положительная пластина одного конденсатора соединяется с отрицательной пластиной следующего конденсатора. В этом случае, заряды на пластинах конденсаторов равны, а обратные напряжения складываются алгебраически.

Теперь, применим эти принципы к данной задаче.

Изображенная на схеме RLC-цепь содержит несколько конденсаторов, соединенных как последовательно, так и параллельно. Для определения эквивалентной емкости цепи, нам необходимо разделить ее на несколько отдельных частей и последовательно анализировать каждую из них.

Для начала, обратим внимание на серию конденсаторов C2, C4 и C6. Они соединены последовательно, поэтому эквивалентная емкость для них может быть вычислена следующим образом:
1/Cэкв(2,4,6) = 1/C2 + 1/C4 + 1/C6

Подставляя значения емкостей конденсаторов, получаем:
1/Cэкв(2,4,6) = 1/1 мкФ + 1/1 мкФ + 1/1 мкФ = 3/1 мкФ = 3 мкФ

Таким образом, эквивалентная емкость для конденсаторов C2, C4 и C6 равна 3 мкФ.

Далее, посмотрим на параллельное соединение, состоящее из конденсаторов C1 и C5. В таком случае, эквивалентная емкость определяется путем сложения емкостей параллельно соединенных конденсаторов:
Cэкв(1,5) = C1 + C5

Подставим значения:
Cэкв(1,5) = 2 мкФ + 3 мкФ = 5 мкФ

Теперь, обратимся к соединению ветвей Cэкв(1,5) и Cэкв(2,4,6). Они соединены последовательно, значит, эквивалентная емкость для них может быть найдена следующим образом:
1/Cэкв = 1/Cэкв(1,5) + 1/Cэкв(2,4,6)

Подставляя значения эквивалентных емкостей, получаем:
1/Cэкв = 1/5 мкФ + 1/3 мкФ

Для сложения дробей с разными знаменателями, нам нужно найти их общее кратное и привести к общему знаменателю. Общим кратным для 5 и 3 является 15:
1/Cэкв = 1/5 мкФ * 3/3 + 1/3 мкФ * 5/5
1/Cэкв = 3/15 мкФ + 5/15 мкФ
1/Cэкв = 8/15 мкФ

Теперь, найдем эквивалентную емкость цепи путем инвертирования полученного значения:
Cэкв = 15/8 мкФ

Итак, эквивалентная емкость цепи (Cэкв) со смешанными соединениями конденсаторов при данных условиях равна 15/8 мкФ или примерно 1,875 мкФ.