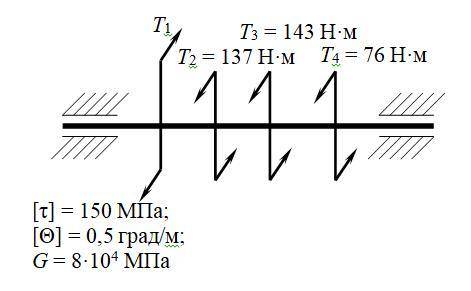
Построить эпюру крутящих моментов для вала по данным своего варианта, показанного на рис. 32. По данным [τ] и [Θ] определить требуемый диаметр вала и округлить его до ближайшего значения из ряда: 30, 35, 40, 45, 50, 60, 70, 80, 90, 100, 110, 125, 140, 160, 180, 200 мм.

Для начала давай разберемся, что такое крутящий момент и эпюра. Крутящий момент - это сила, которая вызывает вращение объекта вокруг оси. Он измеряется в ньютонах на метр (Н·м). Эпюра - это графическое представление зависимости крутящего момента от заданного параметра, в данном случае от диаметра вала.

Перейдем к задаче. Нам даны данные [τ] и [Θ], которые являются значениями крутящего момента и диаметра вала соответственно. Нам нужно определить требуемый диаметр вала и округлить его до ближайшего значения из предложенного ряда.

1. Сначала построим эпюру крутящих моментов для вала по данным своего варианта, показанного на рисунке 32. Для этого возьмем данные [τ] и [Θ] и построим график, где по оси X будут откладываться значения диаметра вала, а по оси Y - значения крутящего момента. Будем соединять полученные точки линией.

2. Теперь перейдем к определению требуемого диаметра вала. Для этого смотрим на график эпюры. Ищем точку, где крутящий момент ([τ]) достигает максимального значения. После этого находим соответствующее значение диаметра ([Θ]) в этой точке.

3. Полученное значение диаметра округляем до ближайшего значения из предложенного ряда: 30, 35, 40, 45, 50, 60, 70, 80, 90, 100, 110, 125, 140, 160, 180, 200 мм.

Итак, шаги решения задачи:

1. Возьми данные [τ] и [Θ]. Построй график эпюры, где по оси X откладываются значения диаметра вала, а по оси Y - значения крутящего момента.

2. Найди на графике точку, в которой крутящий момент ([τ]) достигает максимального значения.

3. Соответствующее значение диаметра ([Θ]) в этой точке будет являться требуемым диаметром вала.

4. Округли требуемый диаметр до ближайшего значения из ряда: 30, 35, 40, 45, 50, 60, 70, 80, 90, 100, 110, 125, 140, 160, 180, 200 мм.

Надеюсь, что объяснение и пошаговое решение задачи были понятными для тебя. Если у тебя возникли еще вопросы, не стесняйся задавать!