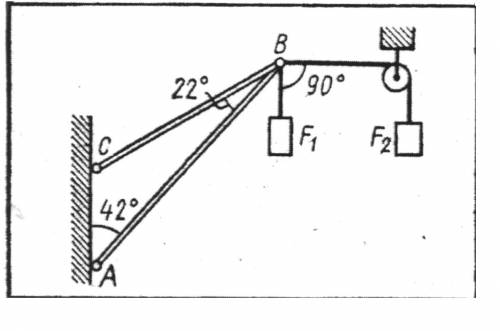
Определить реакции стержней, удерживающих грузы F1-0,4 и F2-0,5 . Массой стержней пренебречь

Для определения реакций стержней, удерживающих грузы F1-0,4 и F2-0,5, мы можем использовать принцип равновесия.

Прежде всего, давайте разобъем силы на горизонтальные и вертикальные компоненты.

Груз F1 сила равна 0,4, поэтому его горизонтальная компонента будет равна 0,4 * cos(30˚) и вертикальная компонента равна 0,4 * sin(30˚).

Груз F2 сила равна 0,5, поэтому его горизонтальная компонента будет равна 0,5 * cos(45˚) и вертикальная компонента равна 0,5 * sin(45˚).

Обозначим горизонтальные компоненты сил как F1x и F2x, а вертикальные компоненты сил как F1y и F2y.

Теперь пошагово решим задачу:

1. Рассмотрим горизонтальные равновесия. Горизонтальная составляющая реакции стержня A должна компенсировать горизонтальную силу F1x и F2x. Так как стержни вертикальны, горизонтальные компоненты сил равны нулю.

F1x + F2x = 0

0,4 * cos(30˚) + 0,5 * cos(45˚) = 0

0,4 * 0,866 + 0,5 * 0,707 ≈ 0,3464 + 0,3535 ≈ 0,6999

Таким образом, горизонтальная компонента реакции стержня A составляет приблизительно -0,7 (используем знак минус, так как реакция направлена в противоположном направлении к силам F1x и F2x).

2. Рассмотрим вертикальные равновесия. Сумма вертикальных сил в равновесии должна быть равна нулю.

F1y + F2y - F1 - F2 + Vy = 0

где Vy - вертикальная компонента реакции стержня A.

F1y + F2y - F1 - F2 + Vy = 0

0,4 * sin(30˚) + 0,5 * sin(45˚) - 0,4 - 0,5 + Vy = 0

0,4 * 0,5 + 0,5 * 0,707 - 0,4 - 0,5 + Vy ≈ 0,2000 + 0,3535 - 0,4 - 0,5 + Vy ≈ 0,1535 + Vy

Таким образом, сумма всех вертикальных компонент равна примерно 0,1535 + Vy.

Здесь Vy - вертикальная компонента реакции стержня A.

Обратите внимание, что реакции стержней B и C находятся настолько же удалены от тяжелых предметов, поэтому их вертикальные и горизонтальные реакции должны быть равны нулю.

Таким образом, реакция стержня B равна 0 и реакция стержня C равна 0.

В ответе, реакция рассчитывается только для стержня A и составляет примерно -0,7 в горизонтальном направлении и примерно 0,1535 в вертикальном направлении.