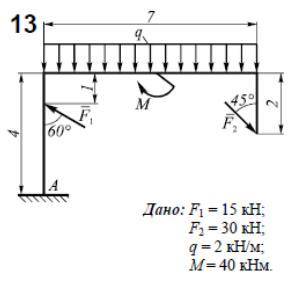
Определить реакции опор рамы

У тебя здесь дана нагруженная рама, и задача состоит в определении реакций опор – т.е. сил, действующих на раму со стороны опор.

Чтобы решить эту задачу, нужно использовать условие равновесия тела. Условие равновесия гласит, что сумма всех сил, действующих на тело в равновесии, равна нулю.

Давай начнем с нахождения горизонтальной компоненты силы реакции опоры в точке A. Поскольку у нас нет горизонтальных сил в системе, реакция в точке A будет нулевой, т.е. Rx = 0.

Теперь обратимся к вертикальной компоненте силы реакции опоры в точке A. Мы видим, что вертикальному равновесию нет силы, которая мешает движению рамы вниз. Значит, реакция опоры в точке A будет равна весу рамы, т.е. Ra = W = mg, где m – масса рамы, g – ускорение свободного падения (около 9,8 м/с²).

Теперь перейдем к определению реакции опоры в точке C. Снова обратимся к условию равновесия. Вертикальная компонента силы реакции опоры в точке C должна компенсировать вес рамы (W), а также силу нагрузки (F). Таким образом, мы можем записать уравнение: Rc - Ra - W - F = 0.

Теперь подставим найденное значение Ra в это уравнение: Rc - mg - F - mg = 0. Таким образом, Rc = F + 2mg.

Наконец, найдем реакцию опоры в точке D. Как и в случае с точкой C, реакция опоры в точке D должна компенсировать вес рамы (W) и силу нагрузки (F). Значит, у нас будет уравнение: Rd = W + F = mg + F.

Таким образом, реакция опоры в точке C равна F + 2mg, а реакция опоры в точке D равна mg + F.