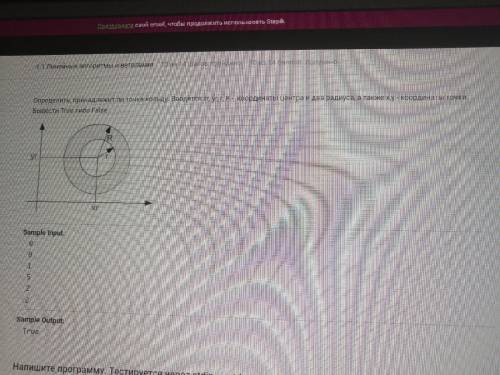
Определить, принадлежит ли точка кольцу. Вводятся xr, yr, r, R - координаты центра и два радиуса, а также x,y - координаты точки. Вывести True либо False. Python

Добрый день! Я буду рад помочь вам разобраться с этим вопросом.

Чтобы определить, принадлежит ли точка кольцу, нам нужно сравнить расстояние от этой точки до центра кольца с радиусами кольца. Если расстояние между точкой и центром кольца входит в интервал между внутренним и внешним радиусами, то точка принадлежит кольцу.

Ниже приведен пример решения на языке программирования Python:

```python
import math

def point_in_ring(xr, yr, R, r, x, y):
# Вычисляем расстояние от точки до центра кольца
distance_to_center = math.sqrt((x - xr) ** 2 + (y - yr) ** 2)

# Проверяем, принадлежит ли точка кольцу
if r < distance_to_center < R:
return True
else:
return False

# Вводим координаты центра и радиусы кольца
xr = float(input("Введите координату x центра кольца: "))
yr = float(input("Введите координату y центра кольца: "))
R = float(input("Введите радиус R кольца: "))
r = float(input("Введите радиус r кольца: "))

# Вводим координаты точки
x = float(input("Введите координату x точки: "))
y = float(input("Введите координату y точки: "))

# Вызываем функцию point_in_ring и выводим результат
if point_in_ring(xr, yr, R, r, x, y):
print("Точка принадлежит кольцу")
else:
print("Точка не принадлежит кольцу")
```

В этом примере мы используем функцию `point_in_ring`, которая принимает координаты центра кольца `xr` и `yr`, радиусы внешнего и внутреннего кругов `R` и `r`, а также координаты точки `x` и `y`. Функция вычисляет расстояние от точки до центра кольца с помощью формулы расстояния между двумя точками в декартовой системе координат.

Затем мы сравниваем это расстояние с радиусами кольца. Если оно больше внутреннего радиуса и меньше внешнего радиуса, то точка принадлежит кольцу и функция возвращает `True`. В обратном случае, точка не принадлежит кольцу и функция возвращает `False`.

Таким образом, мы можем определить, принадлежит ли точка кольцу, используя данную функцию.