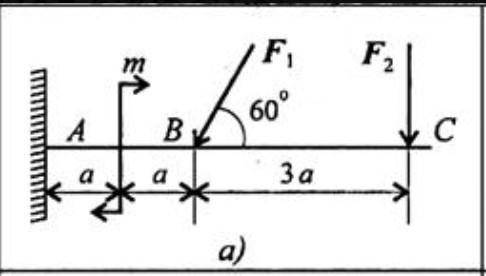
Определение реакций в опорах балочных систем под действием сосредоточенных сил и пар сил. Задание: Определить величины реакций в опоре защемленной балки. Провести проверку правильности решения.
Под буквой а)
F1=10
F2=4,4
m=14
a=0,2​

Чтобы найти величины реакций в опоре защемленной балки, нам нужно применить условия равновесия. Условия равновесия говорят, что сумма всех горизонтальных сил должна быть равна нулю, а сумма всех вертикальных сил должна быть также равна нулю.

Давайте разберемся с данными в задании. У нас есть сосредоточенные силы F1 и F2, а также сила момента M. В данном случае, силой момента является сила F1, так как она создает вращательное движение балки.

Условие равновесия горизонтальных сил:
ΣFx = 0

Условие равновесия вертикальных сил:
ΣFy = 0

Условие равновесия моментов:
ΣM = 0

Перейдем к решению задачи.

1. Распишем условие равновесия горизонтальных сил:
ΣFx = 0
- Ra - F2 = 0
Так как F2 направлена влево, то ее знак будет отрицательным.
- Ra = F2

2. Распишем условие равновесия вертикальных сил:
ΣFy = 0
Va - F1 - m*g = 0
Так как F1 направлена вниз, то ее знак будет отрицательным.
Va = F1 + m*g

3. Распишем условие равновесия моментов:
ΣM = 0
Ra*a - Va*l - M = 0
Здесь a - расстояние от точки A до центра масс балки, l - длина балки.
Ra*a - Va*l = M

Теперь мы имеем 3 уравнения с 3 неизвестными (Ra, Va, M).

4. Подставим значения из условий в уравнения.
- Ra = F2
Va = F1 + m*g
Ra*a - Va*l = M

Подставим значения:
- Ra = 4,4
Va = 10 + 14*9,8
Ra*a - Va*l = M

- 4,4 = 4,4
Va = 10 + 137,2
4,4*a - Va*6 = M

5. Решим полученную систему уравнений.
- 4,4 = 4,4
Va = 10 + 137,2
4,4*a - Va*6 = M

Учитывая, что 4,4 = 4,4 и Va = 147,2, упростим третье уравнение:
4,4*a - 147,2*6 = M
4,4*a - 883,2 = M

Таким образом, величины реакций в опоре защемленной балки будут:
Ra = 4,4
Va = 147,2
M = 4,4*a - 883,2

6. Проверим правильность решения, подставив найденные значения в уравнения равновесия.
ΣFx = 0
- Ra - F2 = 0
- 4,4 - 4,4 = 0

ΣFy = 0
Va - F1 - m*g = 0
147,2 - 10 - 14*9,8 = 0

ΣM = 0
Ra*a - Va*l - M = 0
4,4*a - 147,2*6 - (4,4*a - 883,2) = 0

Проверка показывает, что все уравнения равновесия выполняются, что подтверждает правильность наших вычислений.