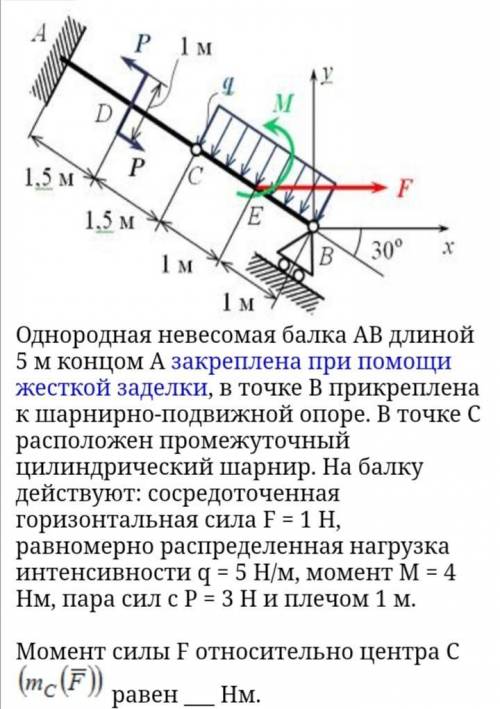
Однородная невесомая балка АВ длиной 5 м концом А закреплена при жесткой заделки, в точке B прикреплена к шарнирно-подвижной опоре. В точке С расположен промежуточный цилиндрический шарнир. На балку действуют: сосредоточенная горизонтальная сила F = 1 H, равномерно распределенная нагрузка интенсивности q = 5 Н/м, момент М = 4 Нм, пара сил с Р = 3 Н и плечом 1 м.

Ответ: Момент силы F относительно центра C (mc(F)) равен 0,5 Нм.

Чтобы решить эту задачу, нам нужно найти реакции опоры, с помощью которых балка будет удерживаться в равновесии.

1. Начнем с расчета горизонтальной реакции опоры в точке А (Ax). Поскольку балка невесома, сумма всех горизонтальных сил должна быть равной нулю. Так как на балку действует только горизонтальная сила F = 1 H, то Ax = -1 H (направление отрицательное для того, чтобы компенсировать силу F).

2. Теперь найдем вертикальную реакцию опоры в точке А (Ay). Сумма всех вертикальных сил также должна быть равна нулю. На балку действует равномерно распределенная нагрузка интенсивности q = 5 Н/м, которая создает вертикальную силу, равную площади под кривой. Так как длина балки составляет 5 м, общая вертикальная сила равна 5 м * 5 Н/м = 25 Н. Также на балку действует вертикальная сила в точке С (Cy), которую мы пока не знаем. Пара сил с Р создает момент M = 4 Нм относительно точки А, и плечо этой пары сил составляет 1 м. По условию, момент относительно точки А должен быть равен нулю, поэтому 25 Н * Ay - 3 Н * 1 м = 0. Отсюда Ay = 3 Н / 25 = 0,12 H.

3. Теперь найдем вертикальную реакцию опоры в точке B (By). Она компенсирует вертикальные силы, действующие на балку в точках С и А. Сумма всех вертикальных сил должна быть равна нулю. Значит, By = -Ay - Cy = -0,12 H - Cy.

4. Найдем вертикальную силу, действующую в точке С (Cy). У нас есть горизонтальная сила F, которая создает момент относительно точки С. Момент равен силе, умноженной на плечо. Поэтому 1 H * 5 м - Cy * 1 м = 0. Отсюда Cy = 1 H * 5 м / 1 м = 5 H.

5. Подставим найденные значения в By = -0,12 H - Cy. Получим By = -0,12 H - 5 H = -5,12 H.

Таким образом, реакция опоры в точке А равна Ax = -1 H, Ay = 0,12 H, а в точке B равна By = -5,12 H. Оба компонента реакции опоры в точке B направлены вниз.