Найти общее решение рекуррентного соотношения 5-го порядка f (n+5)-af (n+4)-bf (n+3)-cf (n+2)-df (n+1)-ef (n) =0
a=-6 b=-6 c=20 d=39 =18
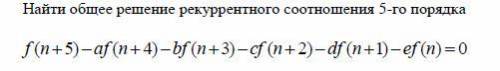
Другие вопросы по теме Другие предметы
Популярные вопросы
- При полном термическом разложении смеси нитратов серебра и меди...
2 - укажіть стрілкою і підпишіть на контурній карті Африка політична...
2 - с 3, 4, 5 номером Задания в фото...
1 - Исследовать функцию и построить ее график: Очень как можно подробнее!...
1 - Срібно-білий активний метал, І повітря боїться він дуже. Є у...
2 - Тело, подброшенное вертикально вверх, поднялось вверх и упало...
2 - Докажите равенство.Теңдікті дәлелдеңіз....
2 - СТАНЦИОННЫЙ СМОТРИТЕЛЬ ДАТЬ ОТВЕТ НА 8 ВОПРОСв зелёной рамке...
1 - У складі армії якої країни воював Легіон українських січових...
3 - Чому навчанню грамота в школі приділяли таку увагу?...
1
Шаг 1: Найдем характеристическое уравнение.
Характеристическое уравнение получается путем замены каждой рекуррентной переменной f(n) на x^n. В данном случае, мы заменяем f(n) на x^n и получаем:
x^5 - ax^4 - bx^3 - cx^2 - dx - e = 0
Шаг 2: Решим характеристическое уравнение.
Подставим значения a, b, c, d и e:
x^5 - (-6)x^4 - (-6)x^3 - 20x^2 - 39x - 18 = 0
x^5 + 6x^4 + 6x^3 - 20x^2 - 39x - 18 = 0
Шаг 3: Разложим характеристическое уравнение на множители.
Мы можем воспользоваться методом синтетического деления, чтобы найти один из корней уравнения. Попробуем найти корень x = 1.
1 | 1 6 6 -20 -39 -18
- 1 5 11 -9 -48
________________________
1 5 11 -9 -48 -66
Шаг 4: Найдем оставшиеся корни.
После применения метода синтетического деления, мы получаем следующее уравнение:
x^4 + 5x^3 + 11x^2 - 9x - 48 = 0
Мы можем попробовать другие значения x, чтобы найти остальные корни уравнения. Применим подбор и найдем корни x = -3 и x = -4.
Таким образом, после нахождения всех корней характеристического уравнения, мы получаем следующие корни: x = 1, x = -3, x = -4.
Шаг 5: Найдем общее решение.
Если у нас есть корни характеристического уравнения, то общее решение будет иметь следующий вид:
f(n) = c1 * x1^n + c2 * x2^n + c3 * x3^n + c4 * x4^n + c5 * x5^n,
где c1, c2, c3, c4 и c5 - произвольные постоянные, а x1, x2, x3, x4 и x5 - корни характеристического уравнения.
Используя корни, которые мы нашли, получаем общее решение:
f(n) = c1 * 1^n + c2 * (-3)^n + c3 * (-4)^n + c4 * 1^n + c5 * 0^n.
Учитывая, что 0^n = 0 для любого значения n, мы можем упростить общее решение:
f(n) = c1 + c2 * (-3)^n + c3 * (-4)^n + c4 + c5 * 0.
Таким образом, общее решение рекуррентного соотношения 5-го порядка f(n+5) - af(n+4) - bf(n+3) - cf(n+2) - df(n+1) - ef(n) = 0 будет иметь вид:
f(n) = c1 + c2 * (-3)^n + c3 * (-4)^n + c4 + c5 * 0.
Где c1, c2, c3, c4 и c5 - произвольные постоянные.