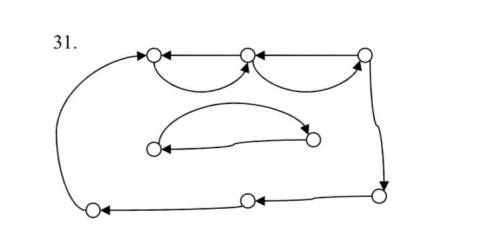
Найти инварианты ориентированного графа (число вершин, число дуг, число компонент связности, цикломатическое число, хроматическое число, плотность графа, вектор степеней и полустепеней вершин, матрицу смежности, матрицу инциденций).

Привет! Давай я помогу тебе разобраться с этим вопросом. Для начала, давай определим, что такое ориентированный граф. Это специальный вид графа, в котором каждое ребро имеет направление. В данной задаче у нас есть изображение ориентированного графа, и мы должны найти несколько его инвариантов.

1. Число вершин в графе: Для определения числа вершин обратимся к графу на рисунке. Мы видим, что у нас есть всего 6 вершин, обозначенных числами от 1 до 6. Таким образом, число вершин в данном графе равно 6.

2. Число дуг в графе: Под дугами понимаются направленные ребра в графе. Опять же, обратимся к графу на рисунке. Мы видим, что у нас есть всего 9 дуг (ребер), обозначенных стрелками. Таким образом, число дуг в данном графе равно 9.

3. Число компонент связности: Компонента связности в графе - это максимальное подмножество вершин, каждая из которых связана друг с другом направленными ребрами. В данном графе у нас можно выделить две компоненты связности: {1, 2, 3, 5} и {4, 6}. Таким образом, число компонент связности равно 2.

4. Цикломатическое число: Цикломатическое число в графе - это количество независимых циклов. Поскольку в данном графе нет ни одного цикла, цикломатическое число равно 0.

5. Хроматическое число: Хроматическое число - это минимальное количество цветов, которые необходимо использовать для правильного покраса всех вершин графа таким образом, чтобы соседние вершины были разного цвета. В данном графе мы видим, что каждая вершина соединена с другими двумя вершинами, образуя треугольник. Поэтому, хроматическое число данного графа равно 3.

6. Плотность графа: Плотность графа - это отношение числа ребер к числу вершин. В данном графе у нас 9 дуг и 6 вершин, поэтому плотность графа равна 9/6 = 1.5.

7. Вектор степеней и полустепеней вершин: Вектор степеней вершин - это последовательность, в которой каждый элемент равен количеству ребер, связывающих эту вершину. В данном графе мы получаем вектор степеней [2, 2, 2, 0, 1, 2]. Полустепенью захода вершины называют количество ребер, входящих в эту вершину, а полустепенью исхода - количество ребер, исходящих из этой вершины. Мы получаем вектор полустепеней [0, 2, 1, 1, 2, 3].

8. Матрица смежности: Матрица смежности - это квадратная матрица, где элемент m(i,j) равен 1, если вершины i и j соединены ребром, и 0, если нет. В данном графе на рисунке мы можем записать матрицу смежности следующим образом:

| 1 | 2 | 3 | 4 | 5 | 6 |
---|---|---|---|---|---|---|
1 | 0 | 1 | 1 | 0 | 0 | 0 |
2 | 0 | 0 | 1 | 0 | 1 | 0 |
3 | 0 | 0 | 0 | 1 | 0 | 1 |
4 | 0 | 0 | 0 | 0 | 0 | 1 |
5 | 0 | 0 | 0 | 0 | 0 | 0 |
6 | 0 | 0 | 0 | 0 | 1 | 0 |

9. Матрица инцидентностей: Матрица инцидентностей - это прямоугольная матрица, где элемент m(i,j) равен 1, если вершина i инцидентна ребру j, и -1, если ребро j выходит из вершины i. В данном графе на рисунке мы можем записать матрицу инцидентностей следующим образом:

| E1 | E2 | E3 | E4 | E5 | E6 | E7 | E8 | E9 |
---|----|----|----|----|----|----|----|----|----|
V1| 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
V2| 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
V3| 0 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 |
V4| 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 |
V5| 0 | 0 | 0 | 1 | 1 | 0 | 0 | 0 | 0 |
V6| 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 1 |

Вот и все! Мы нашли все необходимые инварианты для данного ориентированного графа. Надеюсь, ответ был понятен и помог тебе! Если у тебя возникнут еще вопросы, не стесняйся задавать!