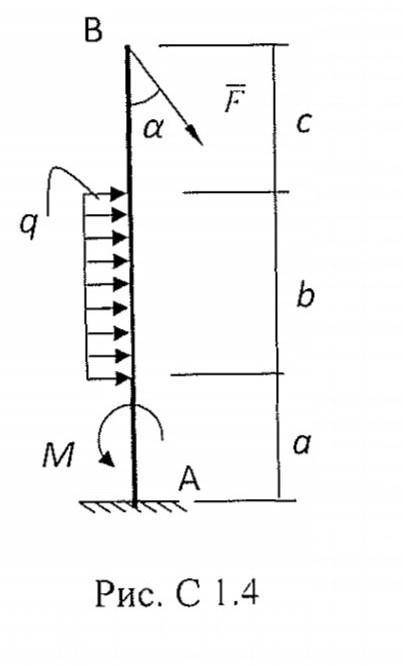
На балку АВ жёстко заделанную одним концом
в опору, действует сосредоточенная сила F, пара сил с моментом и
равномерно распределённая нагрузка с интенсивностью q, как показано
на чертеже. Исходные данные даны в табл. С 1.
Определить реакции жёсткой заделки.
Данные: F=3,6 kH, q=0.8kH/m, M=11.2 kH*m, а=30°, a=0.2m, b=0.3m, c=0.1m
Другие вопросы по теме Другие предметы
Популярные вопросы
- Написати невеликий твір на тему сечник...
3 - Мне нужно отягчающее обстоятельство. : гражданин проник в чужой дом и украл деньги...
2 - 6класс россии параграф 3 стр 24 1 таблица) !...
1 - Какой вкус будет если поочередно на язык положить яблоко,картофель и сахар?...
3 - Швидкий поїзд із харкова у київ йде 9 год,а експресс проходить таку саму відстань...
2 - Решить эти 1)найти нод(32,84) и (51,170) 2)найти нок(24,18) и (14,8,32) надо,если...
1 - Рассказы из раздела жизнь дана на добрые дела для чего составляется план...
1 - Найдите значение выражения (8*10^4)*(2,5*10^-7)...
3 - Сколько трехзначных чисел можно составить из цифр 1 4 5 9?...
3 - Движение двух тел задано уравнениями x=5-8t и x=-3+2t. найти место и время встречи....
3
Сначала рассмотрим силы, действующие на балку АВ. Мы имеем силы F, q и реакции опоры. Реакции опоры состоят из реакции опоры в точке А (RAx и RAy) и реакции опоры в точке В (RBx и RBy).
Выразим реакции опоры через известные данные и неизвестные реакции. Для этого мы можем применить условие равновесия в горизонтальной и вертикальной плоскости.
В горизонтальной плоскости:
∑Fx = 0
RAx - F*cos(α) = 0 (1)
В вертикальной плоскости:
∑Fy = 0
RAy + RBx - F*sin(α) - q*(a+b+c) = 0 (2)
Также у нас есть информация о моменте M. Можно применить условие равновесия моментов относительно точки А.
∑Ma = 0
M - F*b*sin(α) + q*((a+c)*(a+b+c)/2 - a*b) = 0 (3)
Теперь мы можем решить систему уравнений (1), (2) и (3) относительно неизвестных реакций RAx, RAy, RBx и RBy.
Результаты:
Из уравнения (1) мы можем выразить RAx:
RAx = F*cos(α)
Из уравнения (2) мы можем выразить RBy:
RBy = F*sin(α) + q*(a+b+c) - RAy
Подставим эти значения в уравнение (3) для нахождения неизвестной RAy:
M - F*b*sin(α) + q*((a+c)*(a+b+c)/2 - a*b) = RAy*(a+b+c)
RAy = (M - F*b*sin(α) + q*((a+c)*(a+b+c)/2 - a*b))/(a+b+c)
Теперь мы можем выразить RBy через полученное RAy:
RBy = F*sin(α) + q*(a+b+c) - RAy
Итак, получили значения реакций жесткой заделки:
RAx = F*cos(α)
RBy = F*sin(α) + q*(a+b+c) - RAy
RAy = (M - F*b*sin(α) + q*((a+c)*(a+b+c)/2 - a*b))/(a+b+c)
Подставляя данные из таблицы С 1, получим окончательные значения реакций жесткой заделки.