На балку АВ (рис. С 1.0 - С 1.9), жёстко заделанную одним концом
в опору, действует сосредоточенная сила F, пара сил с моментом и
равномерно распределённая нагрузка с интенсивностью q, как показано
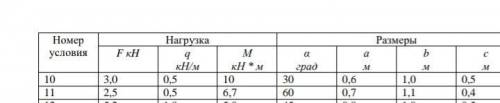
на чертеже. Исходные данные даны в табл. С 1.
Определить реакции жёсткой заделки.
( Номер условия 11)

Другие вопросы по теме Другие предметы
Популярные вопросы
- Определите основную мысль текста....
1 - CAB = 5 CMBC = 11 смР=СМDS = см2...
1 - (Выберите наиболее подходящее слово для предложения) 1. Tins product will help...
2 - Найдите наимешее значение выражения x^2-5x-6 быстр...
2 - Напишите о популярных в нашей стране любительских и профессиональных видах спорта....
3 - 4. В стене имеется маленькая (точечная) дырочка. У хозяина есть флажок, изображённый...
1 - НУЖНО кстати, никаких «сходств, различий» не надо, вот поэтому так легко, и...
2 - Найдите коэффициент k в функции выражающей обратную пропорциональность, если...
1 - 4. На рисунке угол Е = углу Д, АЕ=АД. Докажите, что треугольник МАК - Равнобедренный...
2 - 1. Lucy’s grandfather is always busy. 2. He is retired now. 3. Lucy’s grandfather...
3
Сначала рассмотрим равновесие сил по оси Y. Поскольку балка полностью заделана в опору, реакция опоры в точке А будет направлена вертикально вверх. В то же время, сумма всех вертикальных сил должна быть равна нулю. Следовательно, можем записать уравнение равновесия по оси Y:
RA - F - q * L = 0,
где RA - реакция опоры в точке А, F - сосредоточенная сила, q - интенсивность равномерно распределенной нагрузки, L - длина балки.
Теперь рассмотрим уравнение моментов относительно точки А. Так как заделка жесткая, то сумма моментов должна быть равна нулю. Момент относительно сосредоточенной силы будет равен F * L, а момент относительно равномерно распределенной нагрузки будет равен (q * L^2) / 2. Таким образом, можем записать уравнение моментов:
F * L + (q * L^2) / 2 = 0.
Теперь, имея два уравнения, мы можем решить их относительно неизвестных величин. Для этого сначала найдем значение q из первого уравнения:
q = (RA - F) / L.
Теперь подставим это значение q во второе уравнение:
F * L + ((RA - F) / L) * L^2 / 2 = 0.
Упростим это уравнение:
2F * L + (RA - F) * L = 0,
F * (2L - L) + RA * L = 0,
F * L + RA * L = 0,
(L + L) * RA = -F * L,
2L * RA = -F * L,
RA = -(F * L) / (2L).
Таким образом, реакция опоры в точке А равна RA = -(F * L) / (2L).
Итак, ответ на задачу: реакция опоры в точке А равна RA = -(F * L) / (2L).