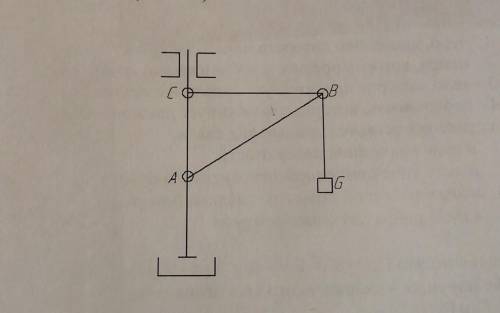
Кран удерживает груз G=20кН. Найти N1 и N2 в стержнях ВС и АС. Если АВ=4м, ВС=3м, АС=2,5м. ​

Для решения данной задачи, нам понадобится использовать условие равновесия моментов и суммы сил по вертикали.

1. Посчитаем моменты сил, действующих на систему относительно точки А.
Вертикальный стержень ВС не нагружен никакими силами, поэтому момент силы N1 равен 0.
Горизонтальный стержень АС также не нагружен силами, поэтому момент силы N2 тоже равен 0.
Момент силы тяжести груза G, действующей на систему сил, равен величине этой силы, умноженной на расстояние от точки А до прямой действия силы G. В данном случае, расстояние равно AC = 2,5 м. Поэтому момент G равен 20 кН * 2,5 м = 50 кН*м.

2. Запишем условие равновесия моментов относительно точки А:
0 + 0 = 50 кН*м
Из этого равенства следует, что N1 = N2 = 0.

3. Суммируем силы по вертикали. На вертикальный стержень ВС действуют сила тяжести груза G и сила реакции опоры в точке В. Поскольку система статически сбалансирована, сумма сил по вертикали должна быть равна 0.
Выразим силу реакции опоры через силу тяжести груза G:
G = N1 + N2
20 кН = N1 + N2

Используя равенство N1 = N2 = 0, подставим значения в уравнение:
20 кН = 0 + 0

Отсюда следует, что N1 = N2 = 0.

Таким образом, сила N1 в стержне ВС и сила N2 в стержне АС равны 0. Это означает, что оба стержня не испытывают никаких внутренних напряжений и выступают в роли пассивных элементов конструкции, не несущих никакой нагрузки.