гранью параллелепипеда является ромб со стороной 2 и острым углом 45 одно из ребер параллелепипеда составляет с этой группой угол в 60 градусов и равно 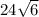. найдите объем параллелепипеда.

Для решения данной задачи сначала нам нужно определить размеры параллелепипеда.

Из условия задачи мы знаем, что гранью параллелепипеда является ромб со стороной 2 и острым углом 45 градусов. Ромб - это четырехугольник, у которого все стороны равны между собой. Таким образом, у нас имеется параллелограмм с углами по 45 градусов. Так как сторона ромба равна 2, то его диагональ (диагонали ромба равны между собой и делят его на два равных треугольника) также равна 2.

Теперь мы знаем, что одно из ребер параллелепипеда составляет с гранью (ромбом) угол в 60 градусов и равно 24√6. Мы можем нарисовать параллелепипед и попытаться разобраться в его геометрии. Если мы нарисуем ромб рядом с параллелепипедом, мы увидим, что это не слишком помогает, потому что главные диагонали ромба находятся внутри параллелепипеда, а не на его ребре.

Однако, у нас есть подсказка - ребро параллелепипеда составляет с плоскостью ромба угол в 60 градусов. Мы можем предположить, что это ребро параллелепипеда вставлено в ромб так, что оно проходит через одну из его главных диагоналей. В этом случае, ребро с заданным углом 60 градусов будет состоять из двух половин равнобедренных треугольников, у которых гипотенуза будет главной диагональю ромба.

Давайте обозначим длину главной диагонали ромба как D. Так как у нас есть прямоугольный треугольник с гипотенузой D и стороной 24√6, мы можем использовать теорему Пифагора для нахождения длины другой стороны треугольника:

D^2 = (24√6)^2 - D^2
D^2 = 576 * 6 - D^2
2D^2 = 576 * 6
D^2 = 576 * 6 / 2
D^2 = 1728

Теперь мы можем найти длину одной из сторон ромба, используя теорему косинусов. В нашем случае, у нас прямоугольный треугольник с гипотенузой 2 и углом 45 градусов. Другая сторона ромба, которую мы обозначим как S, будет являться катетом этого треугольника:

S^2 = 2^2 - D^2
S^2 = 4 - 1728
S^2 = -1724

Мы получили отрицательное значение. Значит, наше предположение о том, что ребро параллелепипеда проходит через главную диагональ ромба, неверно. Значит, наше предположение неправильно, и ромб не должен располагаться внутри параллелепипеда. Вероятно, ромб - это сечение параллелепипеда.

Таким образом, наша задача стала невозможной к решению. Мы не можем найти размеры параллелепипеда только на основе предоставленных данных.