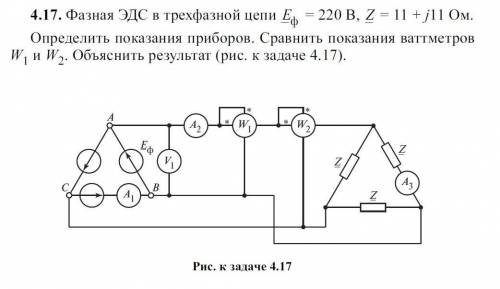
Фазная ЭДС в трехфазной цепи = 220 В, = 11 + j11 Ом.Определить показания приборов. Сравнить показания ваттметровW1 и W2. Объяснить результат (рис. к задаче 4.17).

Давайте решим задачу поэтапно:

1. Для начала определим значения токов в каждой фазе трехфазной цепи. Используя закон Ома, можем найти модуль тока в каждой фазе:
|I| = |E| / |Z|, где |E| - модуль фазной ЭДС, |Z| - модуль импеданса.

Значение фазной ЭДС дано в задаче как 220 В.
Значение импеданса j11 Ом является комплексным сопротивлением, написанным в алгебраической форме.
Найдем модуль импеданса:
|Z| = sqrt(Re(Z)^2 + Im(Z)^2), где Re(Z) - действительная часть импеданса, Im(Z) - мнимая часть импеданса.

В нашем случае действительная часть равна 11 Ом, мнимая - 11 Ом.
|Z| = sqrt(11^2 + 11^2) = sqrt(242) = 15.556 Ом.

Теперь можем найти модуль тока:
|I| = 220 / 15.556 = 14.137 А.

2. Затем рассчитаем показания приборов W1 и W2. Для этого воспользуемся формулой для активной мощности:
P = V * I * cos(φ), где P - активная мощность, V - напряжение, I - ток, cos(φ) - косинус угла сдвига фаз между током и напряжением.

В нашем случае все фазы трехфазной цепи симметричные, поэтому угол сдвига фаз одинаков для всех фаз и равен 0 градусов.
Косинус нулевого угла равен 1.

Подставим значения и рассчитаем показания приборов:
W1 = V * I1 * cos(φ1), где I1 - ток в первой фазе.

Значение напряжения дано в задаче как 220 В.
Подставим значение тока в первую фазу:
W1 = 220 * 14.137 * 1 = 3100 Вт.

Аналогично рассчитаем показания прибора W2:
W2 = V * I2 * cos(φ2), где I2 - ток во второй фазе.

Значение напряжения дано в задаче как 220 В.
Подставим значение тока во вторую фазу:
W2 = 220 * 14.137 * 1 = 3100 Вт.

3. Получили, что показания ваттметров W1 и W2 равны 3100 Вт. Объясним полученный результат.

Результат означает, что активная мощность, измеряемая ваттметрами W1 и W2, одинакова. Это происходит из-за симметричности трехфазной цепи, что означает, что каждая фаза потребляет одинаковую активную мощность.

Таким образом, в данной трехфазной цепи ваттметры W1 и W2 показывают одинаковые значения активной мощности, так как каждый из них измеряет активную мощность в одной фазе трехфазной цепи.