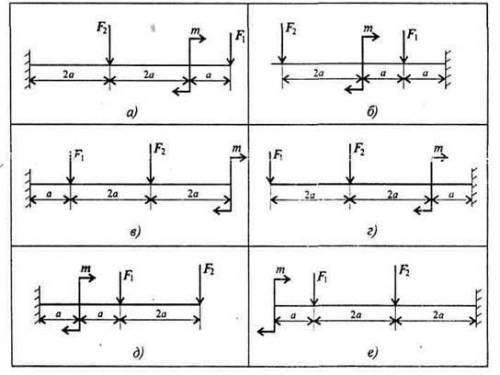
Для одноопорной балки, нагруженной сосредоточенными силами и парой сил с моментом m, построить эпюры поперечных сил и изгибающих моментов. Найти максимальный изгибающий момент и из условия прочности подобрать поперечное сечение для балки в виде двутавра и прямоугольника с соотношением сторон h=2b. Материал балки – сталь, допускаемое напряжение [σ] = 160 МПа. Рассчитать площади поперечных сечений и сделать вывод о целесообразности применения сечения данной формы. Рис. б) Дано F1=24. F2=18. m=6. a=0.5
Другие вопросы по теме Другие предметы
Популярные вопросы
- Соберите материал ободном из заповедников...
1 - Составить рассказ на тему: повседневная жизнь горожанинина 17 века !...
1 - Решить уравнение: 1) (x-1)(x+3)=0 2) (2x-3)^2=0 3) x^2-2x=0 4) x^2+12x+36=0...
1 - Впачке 20 вареников.сьели на 2 меньше,чем осталось.сколько вареников сьели...
3 - Замените в числе 3**5* звездочки четными цифрами так,чтобы полученное...
2 - Какую часть класса составляют девочки(16) мальчиков (11) в ! !...
2 - Склонение по падежам : спорт шебері...
1 - Запишите в виде неравенства.обозначьте неизвестную величину буквой х....
2 - Барбара вышла из дома в 9: 28, а вернулась домой в 14: 15. сколько времени...
1 - Проект по теме семь чудес башкортостана...
1
1. Построим эпюру поперечных сил. Для этого нужно вычислить все вертикальные и горизонтальные силы, действующие на балку. В данном случае у нас есть две силы: F1 и F2.
- Сила F1 направлена вверх и равна 24 Н.
- Сила F2 направлена вниз и равна 18 Н.
- Для определения эпюры поперечных сил, мы учитываем, что узлы балки должны оставаться на месте, поэтому сумма вертикальных сил должна быть равна 0. Таким образом, на эпюре будут отмечены силы F1 и F2, уравновешивающие друг друга.
2. Построим эпюру изгибающих моментов. Для этого нужно вычислить моменты, вызванные силами F1, F2 и парой сил момента m.
- Момент силы F1 относительно точки А равен F1 * a = 24 * 0.5 = 12 Н * м.
- Момент силы F2 относительно точки А равен -F2 * (a + b) = -18 * (0.5 + 1.5) = -54 Н * м (знак "-" говорит о том, что момент направлен против часовой стрелки).
- Момент пары сил m равен m = 6 Н * м и направлен против часовой стрелки.
- На эпюре изгибающих моментов будут отмечены эти три момента.
3. Найдем максимальный изгибающий момент. Для этого нужно проанализировать эпюру изгибающих моментов и найти точку или участок с максимальным значением момента.
- В данном случае, максимальный изгибающий момент будет равен 54 Н * м. Он обусловлен действием силы F2 и находится в середине участка длиной 3 метра.
4. Подберем поперечное сечение для балки. Для этого мы будем использовать двутавр и прямоугольник соответствующих размеров, чтобы обеспечить требуемую прочность материала балки.
- В данном случае, соотношение сторон для прямоугольника h=2b. Положим, что ширина прямоугольника b метров, тогда его высота будет равна h=2b.
- Для двутавра мы можем выбрать подходящий размер, учитывая высоту и ширину балки, чтобы соблюсти условие h=2b.
- Выбор конкретного поперечного сечения будет определяться площадью сечения и его прочностью.
5. Рассчитаем площади поперечных сечений для двутавра и прямоугольника.
- Площадь поперечного сечения двутавра можно вычислить как сумму площадей двух прямоугольников, из которых он состоит.
- Площадь поперечного сечения прямоугольника равна b * h.
6. Сделаем вывод о целесообразности применения сечения данной формы.
- Целесообразность применения сечения данной формы будет определяться сравнением площадей поперечных сечений и допускаемого напряжения материала балки.
- Если площадь поперечного сечения превышает площадь, необходимую для прочности при данном допускаемом напряжении, то применение данной формы сечения будет целесообразным. В противном случае, необходимо выбрать другую форму сечения или увеличить размеры поперечного сечения.
Надеюсь, что этот ответ был подробным и понятным. Если у вас есть еще какие-либо вопросы, не стесняйтесь спрашивать.