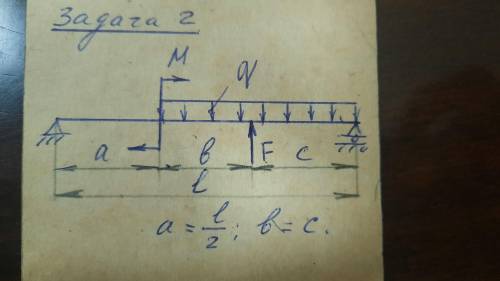
Для двухопорной балки построить эпюры поперечных сил Qy и изгибающих моментов Mx.

Дано:

q=7kH/m

F=10kH

M=15kH×m

l=2m

Для построения эпюр поперечных сил Qy и изгибающих моментов Mx для данной двухопорной балки, мы будем использовать метод моментов.

1. Разобьем балку на несколько участков и назовем их A, B, C, D, E, F, G, H, I, J, K. На каждом участке определим нагрузки и моменты.

На участке AB:

- В точке A имеется вертикальная сила Qy, равная половине нагрузки q, так как на участке AB длина равна l/2. Поэтому Qy = (1/2) * q = (1/2) * 7kH/m = 3.5kH/m.

- Изгибающий момент Mx в точке A равен нулю, поскольку на участке AB не существует моментов.

На участке BC:

- В точке C также имеется вертикальная сила Qy, равная половине нагрузки q, так как на участке BC длина также равна l/2. Поэтому Qy = (1/2) * q = (1/2) * 7kH/m = 3.5kH/m.

- В точке C также имеется и изгибающий момент Mx, который равен моменту от нагрузки F и моменту от силы Qy. Момент от нагрузки равен F * l/2 = 10kH * 2m/2 = 10kH*m. Момент от силы Qy равен Qy * l/2 = 3.5kH/m * 2m/2 = 3.5kH*m. Поэтому Mx = 10kH*m + 3.5kH*m = 13.5kH*m.

На участке CD:

- В точке C сила Qy равна половине нагрузки q, и идеально равна 3.5kH/m.

- В точке D сила Qy также равна половине нагрузки q, но направлена в другую сторону. Поэтому Qy = -3.5kH/m.

- В точке C изгибающий момент Mx равен моменту от нагрузки F, который мы уже вычислили ранее и равен 10kH*m.

- В точке D изгибающий момент Mx равен моменту от нагрузки F и моменту от силы Qy. Момент от нагрузки равен F * l/2 = 10kH * 2m/2 = 10kH*m. Момент от силы Qy равен Qy * l/2 = -3.5kH/m * 2m/2 = -3.5kH*m. Поэтому Mx = 10kH*m - 3.5kH*m = 6.5kH*m.

На участке DE:

- В точке D сила Qy равна половине нагрузки q, а именно -3.5kH/m.

- В точке E сила Qy также равна половине нагрузки q, но в положительном направлении, или +3.5kH/m.

- В точке D изгибающий момент Mx равен моменту от нагрузки F, который мы уже вычислили ранее и равен 10kH*m.

- В точке E изгибающий момент Mx равен моменту от нагрузки F и моменту от силы Qy. Момент от нагрузки равен F * l/2 = 10kH * 2m/2 = 10kH*m. Момент от силы Qy равен Qy * l/2 = 3.5kH/m * 2m/2 = 3.5kH*m. Поэтому Mx = 10kH*m + 3.5kH*m = 13.5kH*m.

Проделаем аналогичные вычисления для остальных участков:

На участке EF: Qy = 3.5kH/m, Mx = 10kH*m.
На участке FG: Qy = 0, Mx = 10kH*m.
На участке GH: Qy = -3.5kH/m, Mx = 6.5kH*m.
На участке HI: Qy = -3.5kH/m, Mx = 3.5kH*m.
На участке IJ: Qy = 0, Mx = 0.

Теперь, используя полученные значения Qy и Mx для каждого участка, мы можем построить эпюру поперечных сил Qy и изгибающих моментов Mx для этой двухопорной балки. Эпюры показывают распределение этих величин вдоль балки от одной опоры до другой.

Затем рисуем горизонтальную ось, представляющую балку, и наносим точки, соответствующие значениям Qy и Mx на каждом участке. Затем соединяем эти точки линиями, чтобы получить эпюры.

В данном случае, эпюра поперечных сил Qy будет начинаться с положительного значения 3.5kH/m, затем уменьшаться до 0 в точке C, становиться отрицательной -3.5kH/m на участке CD, далее уменьшаться до нуля в точке E, и оставаться нулевой на участке FG и IJ.

Эпюра изгибающих моментов Mx будет иметь форму прямоугольника со сторонами 10kH*m, от точки B до D, и от H до J.

Таким образом, получив эпюры поперечных сил Qy и изгибающих моментов Mx, мы сможем лучше визуализировать распределение сил и моментов вдоль балки. Это поможет нам понять, как они влияют на статическую и прочностную характеристику балки и выполнить необходимые расчеты.