Дано: R1 = 16 oм
R2 = - ом
Xl1 = 10 oм
XL2 = 8 ом
Xc1 = 6 om
Xc2 = - om
U = 80
Найти:
1) полное сопротивление Z;
2) напряжение, U приложенное к цепи ;
3) ток ;
3) угол сдвига фаз φ; ( по величине к знаку)
4) активную P, реактивную Q и полную S мощности цепи.
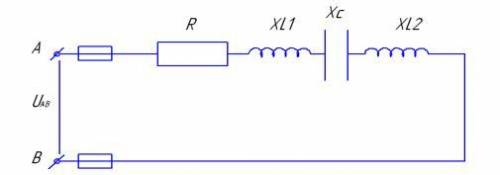
Начертить в маштабе векторную диаграмму цепи и пояснить ее построение.

Для решения данной задачи воспользуемся формулами, связывающими активное сопротивление R и реактивное сопротивление X в комплексном сопротивлении Z:

Z = R + jX,

где j - мнимая единица, такая что j^2 = -1.

1) Полное сопротивление Z:
Задано, что R1 = 16 ом, Xl1 = 10 ом, Xc1 = 6 ом, R2 = - ом и Xl2 = 8 ом, Xc2 = - ом. Очевидно, что значение R2 и Xc2 не даны, следовательно, мы не можем рассчитать полное сопротивление Z. Необходимы дополнительные данные для решения этого вопроса.

2) Напряжение U приложенное к цепи:
Задано, что U = 80 В. Напряжение U приложенное к цепи равно величине комплексного сопротивления Z, так как в этом случае цепь находится в равновесии. Значит, U = |Z| = |R + jX|, где |...| обозначает модуль комплексного числа. В нашем случае, U = |16 + j(10 - 8)| = |16 + j2| = sqrt(16^2 + 2^2) = sqrt(260) = 2sqrt(65) В.

3) Ток:
Ток в цепи можно рассчитать, используя формулу Ohm's law: I = U / Z, где U - напряжение и Z - полное сопротивление. Однако, без известного значения Z мы не можем точно рассчитать ток.

4) Угол сдвига фаз φ и мощность:
Угол сдвига фаз φ можно найти, используя следующее соотношение: tan(φ) = X / R, где X и R - реактивное и активное сопротивления соответственно. Но, поскольку R2 и Xc2 не даны, мы не можем рассчитать угол сдвига фаз.

Активная P, реактивная Q и полная S мощности цепи можно рассчитать, используя следующие формулы:

P = U * I * cos(φ),
Q = U * I * sin(φ),
S = U * I,

где U, I и φ - напряжение, ток и угол сдвига фаз соответственно. Но, поскольку нам неизвестны значения тока и угла сдвига фаз, мы также не можем рассчитать мощности.

Векторная диаграмма цепи строится на комплексной плоскости, где горизонтальная ось представляет активное сопротивление, а вертикальная ось - реактивное сопротивление. Векторное представление импеданса Z будет иметь следующий вид: Z = R + jX. Начертите на плоскости горизонтальный отрезок, представляющий активное сопротивление (16 ом) и вертикальный отрезок, представляющий реактивное сопротивление (2 ом). Соедините концы отрезков и получите векторное представление Z. Теперь, чтобы построить векторную диаграмму для напряжения U, умножьте вектор Z на U, и на комплексной плоскости начертите горизонтальный и вертикальный отрезки, представляющие комплексное напряжение U.

К сожалению, без дополнительных данных мы не можем решить данную задачу полностью. Необходимо знать значения R2 и Xc2 для рассчета полного сопротивления и дальнейшего решения задачи.