Дано: F1, kH = 10
F2, kH = 4,4
m, kH • м = 8
a1M = 0,2

(это техническая механика)
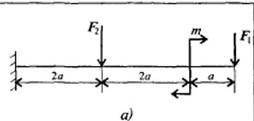
Нужно найти максимальный изгибающий момент (схема ещё должна быть)

ЗА РЕШЕНИЕ​

Добрый день!

Чтобы найти максимальный изгибающий момент в данной задаче, необходимо использовать условие равновесия. Для этого проведем анализ каждого элемента схемы и суммируем моменты вокруг одной точки.

1. Распределим систему на отдельные элементы схемы:
- Палочка силы F1 находится на расстоянии x1 от оси O.
- Палочка силы F2 находится на расстоянии x2 от оси O.
- Масса m находится на расстоянии xm от оси O.
- Момент M1 действует вокруг оси O1, которая находится на расстоянии a1 от оси O.

2. Запишем условие равновесия вращающих моментов:
ΣM = 0, где ΣM - сумма моментов вокруг точки O.

3. Рассмотрим каждый элемент схемы подробнее:

- Палочка силы F1:
Момент M1 = F1 * x1 (так как палочка левее оси O, то момент считается положительным)

- Палочка силы F2:
Момент M2 = F2 * x2 (так как палочка правее оси O, то момент считается отрицательным)

- Масса m:
Момент M3 = m * g * xm (где g - ускорение свободного падения, m * g - сила тяжести)

4. Запишем условие равновесия:
ΣM = M1 + M2 + M3 = 0

5. Подставим известные значения в формулу и решим получившееся уравнение:
F1 * x1 - F2 * x2 + m * g * xm = 0

Учитывая, что F1 = kH * F2 (из условия), а для данной задачи kH = 10, получим:
10 * F2 * x1 - F2 * x2 + m * g * xm = 0

Также у нас известно, что m = 8 кг и a1M = 0,2. Анализируя схему, видно, что расстояние между осью O1 и осью O равно a1 + x1.
Поэтому можем записать xm = a1 + x1. Подставим в уравнение:
10 * F2 * x1 - F2 * x2 + 8 * g * (a1 + x1) = 0

6. Решим полученное уравнение относительно x2:
10 * F2 * x1 + 8 * g * (a1 + x1) = F2 * x2
10 * F2 * x1 + 8 * g * a1 + 8 * g * x1 = F2 * x2
10 * F2 * x1 + 8 * g * a1 + 8 * g * x1 - F2 * x2 = 0
(10 * F2 + 8 * g) * x1 + (8 * g * a1 - F2) * x2 = 0

7. Ответ:
Максимальный изгибающий момент достигается, когда вторая палочка силы F2 находится на расстоянии x2 = (8 * g * a1) / F2 от оси O.

Для того чтобы получить конкретное числовое значение, нужны известные значения g и F2. Также, для получения более точного решения, необходимо знать значения численных коэффициентов a1 и F2.

Надеюсь, данное объяснение и решение помогли вам понять задачу и найти искомый максимальный изгибающий момент. Если возникнут еще вопросы - обращайтесь!