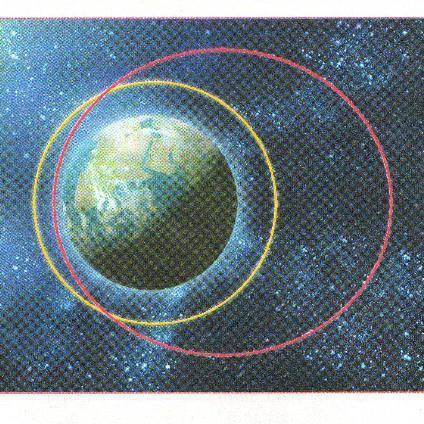
1) На рисунке показаны орбиты двух спутников. Спутник 1 движется по круговой орбите на высоте 2000 км от поверхности Земли. Орбита спутника 2 - эллипс с большой полуосью 9000 км. Плоскости орбит и направление движения совпадают. Могут ли спутники столкнуться? 2) Не производя вычислений, определите, какой спутник 1 или 2 имеет большую скорость в местах возможного столкновения. ответ поясните.
3) Определите радиус R орбиты спутника 1 в м.
4) Вычислите скорость спутника 1 в м/с.
5) Определите, на каком расстоянии r от центра Земли находился спутник 2 в момент столкновения (ответ в м).
6) Вычислите скорость спутника 2 в м/с.
7) Рассчитайте скорость сближения спутников в м/с.

1) Для того чтобы определить, могут ли спутники столкнуться, необходимо проверить, пересекаются ли их орбиты. В данном случае, орбита спутника 1 представляет собой круговую орбиту, а орбита спутника 2 - эллипс. Для того чтобы определить, пересекаются ли они, нужно узнать, есть ли у них общие точки.

Мы знаем, что плоскости орбит и направление движения спутников совпадают, поэтому спутники имеют одинаковую плоскость орбиты. Однако, чтобы определить, пересекаются ли их орбиты, нужно знать взаимное положение их орбит в трехмерном пространстве. Поэтому с помощью данной информации нельзя однозначно сказать, могут ли спутники столкнуться.

2) Для определения, какой спутник имеет большую скорость в местах возможного столкновения, необходимо учесть, что спутник движется по эллиптической орбите, а спутник 1 движется по круговой орбите. На эллиптической орбите скорость спутника не является постоянной и изменяется в разных точках орбиты. В то же время, на круговой орбите скорость спутника постоянна.

Следовательно, спутник 1 имеет большую скорость во всех точках своей орбиты в сравнении с спутником 2.

3) Чтобы определить радиус R орбиты спутника 1, нужно учесть, что спутник движется по круговой орбите на высоте 2000 км от поверхности Земли. Радиус орбиты спутника 1 равен сумме радиуса Земли и высоты орбиты спутника:

R = r_земли + h_орбиты

где r_земли - радиус Земли (приближенно 6371 км), h_орбиты - высота орбиты спутника (2000 км).

R ≈ 6371 км + 2000 км = 8371 км.

4) Для вычисления скорости спутника 1 в м/с, необходимо учесть, что его скорость определяется радиусом его орбиты и периодом обращения. Для круговой орбиты скорость спутника вычисляется по формуле:

V = 2πR / T

где V - скорость спутника, R - радиус орбиты спутника (8371 км), T - период обращения спутника по орбите.

Период обращения спутника можно вычислить по формуле:

T = 2π√(R^3 / GM)

где G - гравитационная постоянная, M - масса Земли.

Данные для точной оценки периода обращения и скорости спутника не предоставлены в вопросе. Поэтому, чтобы сделать приближенные расчеты, можно использовать следующие данные:
G ≈ 6.67 * 10^(-11) м^3/(кг*с^2)
M ≈ 5.97 * 10^24 кг

Подставив значения в формулу для периода обращения и в формулу для скорости, можно получить приближенный результат.

5) Чтобы определить, на каком расстоянии r от центра Земли находился спутник 2 в момент столкновения, необходимо учесть, что спутник движется по эллиптической орбите. В данном случае, мы не располагаем информацией о точном положении спутника 2 в момент столкновения, поэтому точно определить r невозможно.

6) Для вычисления скорости спутника 2 в м/с, также необходимо учесть, что его скорость изменяется в разных точках эллиптической орбиты. Без точных данных о периоде обращения и радиусах орбиты, точно вычислить скорость невозможно.

7) Для расчета скорости сближения спутников в м/с, необходимо знать скорости каждого из спутников и направление их движения.

Из предыдущих пунктов следует, что мы не располагаем всей необходимой информацией для точных вычислений. Для более точного расчета и ответа на этот вопрос, необходимо получить дополнительные данные о периодах обращения, радиусах орбит и скоростях спутников.