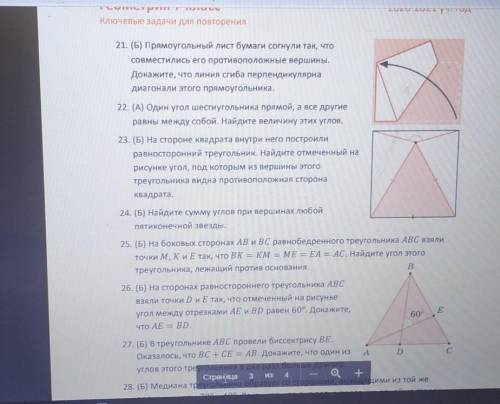
Ключевые задачи для повторения 21. (Б) Прямоугольный лист бумаги согнули так, что
совместились его противоположные вершины.
Докажите, что линия сгиба перпендикулярна
диагонали этого прямоугольника.
22. (А) Один угол шестиугольника прямой, а все другие
равны между собой. Найдите величину этих углов.
23. (Б) На стороне квадрата внутри него построили
равносторонний треугольник. Найдите отмеченный на
рисунке угол, под которым из вершины этого
треугольника видна противоположная сторона
квадрата.
24. (Б) Найдите сумму углов при вершинах любой
пятиконечной звезды.
25. (Б) На боковых сторонах AB и ВС равнобедренного треугольника АВС взяли
точки M, КиЕ так, что ВК = КМ = ME = EA = .AC. Найдите угол этого
треугольника, лежащий против основания.
В
26. (Б) На сторонах равностороннего треугольника АВС
взяли точки D и E так, что отмеченный на рисунке
угол между отрезками AE и BD равен 60°. Докажите,
что AE = BD.
60°
с
27. (Б) В треугольнике ABC провели биссектрису BЕ.
Оказалось, что вс + СЕ = AB. Докажите, что один из A
углов этого треугольника в два раза больше другого.
Страница 3
+
28. (Б) Медиана треугольника образует со сторонами, выходящими из той же
ИЗ
4
нар ора
2
а​

21. Для доказательства того, что линия сгиба является перпендикулярной диагонали прямоугольника, можно воспользоваться следующими рассуждениями.
При сгибе прямоугольного листа бумаги противоположные вершины должны совпасть. Это значит, что линия сгиба будет проходить через обе противоположные вершины.
Также, диагональ прямоугольника соединяет две противоположные вершины. Следовательно, линия сгиба будет пересекаться с диагональю и образовывать угол.
Для доказательства перпендикулярности этих линий, можно воспользоваться теоремой о перпендикулярности.
Теорема: Если две прямые пересекаются и образуют смежные углы, то они перпендикулярны.
В данном случае, линия сгиба пересекает диагональ прямоугольника и образует угол с ней. Этот угол является смежным с одним из углов, образованных диагональю с прямыми сторонами прямоугольника (так как углы, образованные диагональю, являются смежными).
Следовательно, линия сгиба и диагональ прямоугольника пересекаются и образуют смежные углы, значит, они перпендикулярны.

22. Угол шестиугольника прямой, значит, он равен 90 градусам. Другие углы равны между собой.
Поскольку сумма всех внутренних углов многоугольника равна (n-2) * 180 градусов, где n - количество углов в многоугольнике, мы можем использовать эту формулу для шестиугольника: (6-2) * 180 = 4 * 180 = 720 градусов.
Если один угол равен 90 градусов, то остальные пять равны между собой.
Таким образом, каждый из остальных пяти углов равен (720 - 90) / 5 = 630 / 5 = 126 градусов.

23. Чтобы найти угол, под которым из вершины равностороннего треугольника видна противоположная сторона квадрата внутри него, можно провести линию от вершины треугольника к центру квадрата.
Так как равносторонний треугольник имеет все стороны одинаковой длины, это значит, что отрезок, проведенный от вершины треугольника к центру квадрата, равен стороне квадрата.
Так как все углы равностороннего треугольника равны 60 градусов, то угол, под которым из вершины треугольника видна противоположная сторона квадрата, также равен 60 градусов.

24. Чтобы найти сумму углов при вершинах пятиконечной звезды, можно воспользоваться следующими рассуждениями.
Пятиконечная звезда состоит из пяти равнобедренных треугольников, объединенных через их вершины.
Для каждого равнобедренного треугольника, сумма внутренних углов составляет 180 градусов. Два угла равны между собой, потому что это углы оснований равнобедренного треугольника.
Следовательно, каждый из равнобедренных треугольников имеет два равных угла, каждый из которых равен (180 - 180) / 2 = 0 градусов.
Так как у пятиконечной звезды пять равнобедренных треугольников, сумма углов при ее вершинах равна 5 * 0 = 0 градусов.

25. Чтобы найти угол треугольника, лежащий против основания, мы можем воспользоваться следующими рассуждениями.
Из условия задачи известно, что точки M, К и Е разделяют боковые стороны AB и ВС равнобедренного треугольника так, что ВК = КМ = ME = EA = AC.
Так как ВК = КМ = ME = EA, это значит, что все стороны треугольника АВС равны, и, следовательно, он является равносторонним треугольником.
У равностороннего треугольника все углы равны 60 градусов, поэтому угол, лежащий против основания, также равен 60 градусов.

26. Для доказательства того, что AE = BD, можно воспользоваться следующими рассуждениями.
Из условия задачи известно, что на сторонах равностороннего треугольника АВС взяты точки D и E так, что угол между отрезками AE и BD равен 60 градусов.
Так как треугольник АВС является равносторонним, то все его стороны равны друг другу.
Также, у равностороннего треугольника все углы равны 60 градусов.
Таким образом, угол ADB равен углу ADC, который равен 60 градусам.
Также, угол ADC и угол ACD, оба соответствующие углы, равны 60 градусов.
Это значит, что треугольники ADE и ABD равнобедренные.
Так как у равнобедренного треугольника основание разбивается высотой на две равные части, это значит, что AE = BD.

27. Для доказательства того, что один из углов треугольника ABC в два раза больше другого, можно воспользоваться следующими рассуждениями.
Из условия задачи известно, что в треугольнике ABC проведена биссектриса BE, так, что CE + BE = AB.
Мы знаем, что биссектриса делит противолежащую сторону на отрезки, пропорциональные двум оставшимся сторонам.
Так как CE + BE = AB, это значит, что длина отрезка CE + длина отрезка BE равны длине отрезка AB.
Получается, что CE/AB + BE/AB = 1, или CE/AB = 1 - BE/AB.
Так как соотношение CE/AB равносильно соотношению AC/BC (потому что эти отрезки делятся одной прямой, в данном случае, биссектрисой), это значит, что AC/BC = 1 - BE/AB.
Теперь мы можем воспользоваться известным соотношением для биссектрис в треугольнике:
AC/BC = AB/BE.
Подставив это соотношение в предыдущее равенство, мы получаем:
AB/BE = 1 - BE/AB.
Переставим члены:
BE/AB + BE/AB = 1.
Сокращаем на BE:
2BE/AB = 1.
Переносим BE влево и AB вправо:
BE = AB/2.
Таким образом, отрезок BE равен половине стороны AB.
Так как BE является биссектрисой треугольника ABC, это значит, что угол ABC равен углу ACB. Они равны, поскольку биссектриса делит угол на два равных угла.
Таким образом, угол ABC в два раза больше угла ACB.