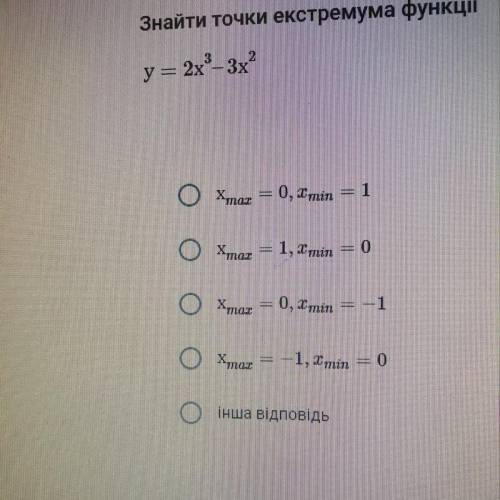
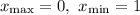Знайти точки екстремума функції
Другие вопросы по теме Алгебра
Популярные вопросы
- Какой год был раньше, и на сколько. 150 год до нашей эры и 150 год нашей...
3 - Розташуйте території у порядку їх завойовування Александром Македонським...
3 - Что нарисовано на 2, 4, 5, 6?...
3 - Решить уравнение из задачи.Через дискриминант 180/x+2 - 180/x=1 по...
1 - 89-700 третий класс. Вычисли, сделай проверку....
3 - A Secret Seven Meeting It was summer. The Secret Seven Society (1. have)...
3 - Чому вода виштовхує нас на поверхню надо...
2 - Великое переселение народов-это... УМОЛЯЮ сделать это задание,только...
1 - Посадил дед репку. Выросла репка большая-пребольшая. Вытащил дед с репку...
2 - У ДВУХ ДЕВОЧЕК БЫЛО 210 КАЛЕНДАРИКОВ .ЕСЛИ ПЕРВАЯ ОТДАСТ 40 ВТОРОЙ ТО...
3
Необходимые условия экстремума:
Имеем две критические (стационарные) точки: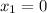 и
и 
Достаточные условия экстремума: если при переходе через критическую точку производная непрерывной функции меняет знак на противоположный, то имеем экстремум функции в этой точке.
Если точка с абсциссой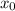 меняет знак с "+" на "–" (двигаясь в направлении увеличения
меняет знак с "+" на "–" (двигаясь в направлении увеличения  ), то
), то 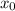 — точка максимума, а если с "–" на "+" , то
— точка максимума, а если с "–" на "+" , то 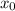 — точка минимума.
— точка минимума.
Из промежутка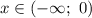 выберем, например,
выберем, например, 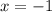 и имеем:
и имеем: 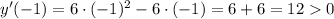
Из промежутка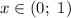 выберем, например,
выберем, например, 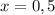 и имеем:
и имеем: 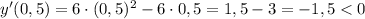
Имеем максимум в точке с абсциссой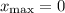
Из промежутка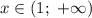 выберем, например,
выберем, например, 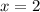 и имеем:
и имеем: 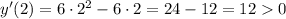
Имеем минимум в точке с абсциссой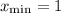
ответ: