Знайти суму перших шести членів геометричної прогресії (bn) якщо b2=12,b4=-6
Другие вопросы по теме Алгебра
Популярные вопросы
- Основной источник загрязнения окружающей среды в восточном казахстане...
3 - Септык деген не ? жыктык тауелдык деген не ?...
2 - Раздели объекты на две группы. запиши название в соответствующие клетки таблицы....
1 - Впиши пропущенное слово. вот мчится прохожих не боится. на хвост лишь наступите-оставит...
3 - Придумайте по 2 предложения со словами: разбилось, сломалось, отвалилось....
1 - Моя родная сторона, смоленщина моя написать сочинение на эту тему...
3 - По музыке построить в тональности a dur s64,d64,t6,t64,s6,d6,t53...
1 - Учимся сочинять.составьте текст-повествование на одну из тем: однажды ранним...
2 - сторон общественой жизни,осушествляемые властью,называетьс?...
3 - Птицы весну принесли . запишите нераспрастраненные предложения...
1
ответ: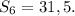
Объяснение: