Знайти суму чотирьох перших членів геометричної прогресії , якщо b2 = 25, b4=1, q< 0
Другие вопросы по теме Алгебра
Популярные вопросы
- Выберите слова в которых мягкость согласного звука обозначена только гласными...
2 - Составьте простое распространённое с однородными членами предложение про...
2 - Как учёный в.и вердадский назвал совокупность всех живых организмов на земле?...
1 - Сократите дробь 36с^2-60с+25 : 25-36с^2 это дробь деление вместо...
2 - Какое проверочное слово в слове-рыжей,усердные? !...
2 - Информационное сообщение на языке, первоначально записанное в 8- битовом...
2 - Соедините слова и звуки, которые в них встречаются bab, bed, jump, run, hen,...
2 - Какая степень сравнения у прилагательного пугливый...
3 - Отрезок длинной 90мм разделили сначала на 3 равный части, а затем каждую...
3 - Понять, как тут решать с модулем. в нужно построить график следующей функции:...
2
Відповідь:
так как по условию q<0
то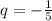
Пояснення: