Знайти площу прямокутника, якщо його периметр дорівнює 274 см, а діагональ дорівнює 97 см.

Ширина прямоугольника равна 65 см.

Длина прямоугольника равна 72 см.

Объяснение:

x — ширина прямоугольника (в см)

y — длина прямоугольника (в см)

Составляем систему:

2y = 274 - 2x

y = 137 - x

x² + (137 - x)² = 9 409

x² + x² - 274x + 18 769 = 9 409

2x² - 274x + 9 360 = 0

x² - 137x + 4 680 = 0

D = 18 769 - 18 720 = 49

x₁ =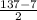 = 65

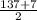x₂ =   = 72