1. Алгебра
  2. Знайти кутовий коефіцієнт дотичної

Знайти кутовий коефіцієнт дотичної до графіка функції f(x) = 6 tg x - 3 ctg x у точці з абсцисою х0 = π ⁄ 3

Nastya0012005 Nastya0012005    2   29.03.2020 15:30    1

Ответы
sevostyanova3064 sevostyanova3064  12.10.2020 08:27

28

Объяснение:

Угловой коэффициент касательной равен производной функции в этой точке.

1. Найдем производную функции.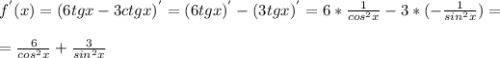f^{'}(x) = (6tgx - 3 ctgx)^{'} = (6tg x)^{'} - (3tg x)^{'} = 6* \frac{1}{cos^{2}x } - 3* (-\frac{1}{sin^{2}x } ) =\\\\= \frac{6}{cos^{2}x } + \frac{3}{sin^{2}x }

2. Подставим значение абсциссы в полученную производную функции:

f^{'} (\frac{\pi }{3} ) = \frac{6}{cos^{2}\frac{\pi }{3} } + \frac{3}{sin^{2} \frac{\pi }{3} } = \frac{6}{(\frac{1}{2} )^{2} } + \frac{3}{(\frac{\sqrt{3} }{2} )^{2} } = \\\\= \frac{6}{\frac{1}{4} } + \frac{3}{\frac{3}{4} } = 6*\frac{4}{1} + 3*\frac{4}{3} = 24 + 4 = 28

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Алгебра
Filip1is Filip1is  21.08.2019 19:10
1+8x+16x^2=0 2x^2-9+4=0 5a^2+216a-24=0 7x^2-2x+12=0 3x^2-5x=0...
OLZHAS1808 OLZHAS1808  21.08.2019 19:10
выручайте у нас уже 12 ночи спать хочу мозги тупят .найдите значение выражения a(7a++3b) при а=√5 b =√3...
mit210404 mit210404  21.08.2019 19:10
Сократите дробь: 3а-2√6ав+2в/√27а³-√8в³...
али419 али419  21.08.2019 19:10
Выпишите первые пять членов арифметической прогрессии(аn), если: а) a1=10, d=4;...
radzihovskaa radzihovskaa  21.08.2019 19:10
Докажите тождество (tga-sina)(cos²a/sina+ctga)=sin²a...
Kiko2802 Kiko2802  21.08.2019 19:10
Замени t одночленом так, чтобы получился квадрат двучлена t2+5x+36x2...
stiles1996 stiles1996  21.08.2019 19:10
Укажите в квадратном уравнении коэффициент a, 7x-5-x^2=0 1.) -1 2.) 1 3.) 7 4.) -5...
xalmatovr xalmatovr  21.08.2019 19:10
Выпишите первые пять членов арифметической прогрессии(аn), если: а) a1=10, d=4; б)a)a1=30, d=-10 ; в)а1=1,7, d=-0,2; г) a 1=-3,5 d=0,6....
мамаТВ мамаТВ  21.08.2019 19:10
Объясните как решить 6*2 корня из 2...
fftoes fftoes  21.08.2019 19:10
Кобщему знаменателю 7 класс. 1 n²+2n+1 и 5n n+1 и n+1 n-1...

Популярные вопросы