Знайти два числа,сума яких дорівнює 10,а сума їх квадратів-58.
9класс
Другие вопросы по теме Алгебра
Популярные вопросы
- Сравни былины с народными сказками. В чем их сходство и отличие? Можешь выполнить...
1 - Предложение на тему Климат с причастием...
1 - ОЧЕНЬ Определи школу, которая относится к казахской традиционной певческой школе.aАлматинская...
2 - Напишите гидролиз соли в том числе в ионных формах Na2S...
3 - Решите уравнение -7(x-5)=18+2(3x+2)...
3 - Тіктөртбұрыштың ұзындығы 9 см, ені 8 см. Осы тіктөртбұрыштың ұзындығы 12 см болып,...
2 - Массасы 20грамм мыс сульфаты бар ерітіндісін массасы 8грамм натрий гидроксидінің...
2 - Сравнительные свойства чистых веществ и железно-серной смеси Признаки сравненияЧистое...
3 - 2 10.4.7 Read again and choosefrom the sentences A-F the onewhich fits each gap...
1 - Мұнай толтырылған цистеранаға 4м тереңдікте , ауданы 30см шүмек бекітілген . Мұнай...
3
Пояснювання:
Нехай числа дорівнюватимуть х и у. ⇒
Відповідь: 3 та 7.
Рiвняння:
1)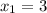 =>
=> 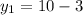
2)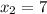 =>
=> 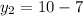
Вiдповiдь: (3; 7); (7; 3)