Знайти cos(a+b), якщо ctg a= -4\3 , ctg b=4\3
Ответы
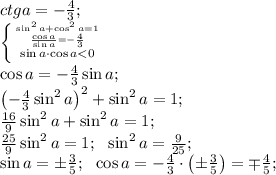
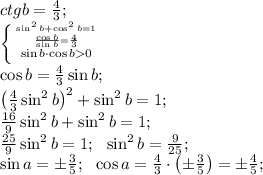 тогда имеем
тогда имеем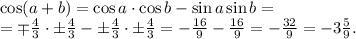
Другие вопросы по теме Алгебра
Популярные вопросы
- 3) Tom for two hours before his parents came home. a ) slept b) was sleeping c)...
2 - Визначити силу струму в провіднику довжиною 20 см, розташованому перпендикулярно...
2 - 4. «Козаки високі на зріст, вправні, енергійні, люблять ходити в гарному одязі......
3 - 1.А) Сравните аэробное и анаэробное дыхание.1Б). Приведите пример двух видов спорта,...
3 - сумативное оценивание за раздел 6.2.А Вещества и материалы 6 класс за 2 четверть...
3 - Теплоізоляційна функція вуглеводів...
2 - Выпишите слова, употребленные в переносном смысле. Кругом, покорив все своей темнотой,...
3 - 1- 1,5+:x + 4,5) 17 = 015. x + 4,5=0 02...
1 - Балқаш көне түрлі тіліндер қандай мағынаны білдіреды умоля...
3 - О чём заставляет задуматься произведение Гоголя ночь перед рождеством? Чему научил?...
2