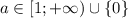Знайдыть множину всіх значень а при яких виконується рівність
|a^3-a^2|=a^3-a^2
Другие вопросы по теме Алгебра
Популярные вопросы
- Какое изобразительно-выразительное средство языка использует А.П. Платонов в...
2 - Французкий- 5 класс В.Н.Шацких 1 часть упр 5 страница 86...
2 - Смешанное питание с преобладанием снегового имеют реки Выберите один ответ:...
2 - Признаком, какого заболевания, передающегося половым путём, является появление...
3 - докажите, что прямая, содержащая середины 2 параллельных хорд окружности, проходит...
2 - Полушария большого мозга-это образования чего....
3 - Может ли энергия связи ядра равняться - 13,3452*10^-11??? я не знаю, правильно...
1 - мне,я могу с балкона сбросится......
2 - Он живет самостоятельно прикрепляясь к почве ризоидами....
2 - На плане расстояние между двумя деревнями составляет 5,2 см. Чему равно расстояние...
3
Модуль числа - это абсолютная величина, то есть величина, принимающая только неотрицательные значения.
Для того чтобы раскрыть модуль, пользуются таким правилом:
В равенстве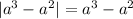 получаем следующее:
получаем следующее:
Решим данное неравенство методом интервалов:
Получили интервал: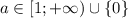 (см. вложение).
(см. вложение).
ответ: