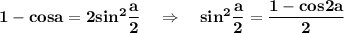Знайдіть значення виразу 3 sin 9°-5cos0°
Другие вопросы по теме Алгебра
Популярные вопросы
- Ваванни і рідколісся південної америки...
3 - Составить рассказ на языке 5 класс мой день из 13 предложений...
3 - Вкаком году начался поход ермакаи и присоединении сибири?...
3 - Представте следующею информацию в наиболее наглядной с вашей точки...
1 - Монолог о любимом месте в доме.где-то 10 предложений...
3 - Какие из данных утверждений верны? запишите их номера. 1) площадь...
3 - Диагонали прямоугольной трапеции взаимно перпендикулярны. найти...
2 - На карте пелепоннеса отметь стрелкой направление вторжения дорийцев,...
2 - Антилопа отталкивается от земли со скоростью 12м/с. на какую высоту...
3 - Продолжите 1.заряд протекающий по проводнику 2. из закона ома напряжение...
1
Вычислим значение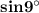 , зная что
, зная что
Применим формулу :