Знайдіть усі натуральні значення x та y, які задовольняють рівняння 3x + 2y = 30. У відповідь запишіть кількість таких пар.
Другие вопросы по теме Алгебра
Популярные вопросы
- Вычислите a) 1/2*2/3/1/3 b) 5/8/3/4*1/2 b) 1/1/2*1/6 г) 1/4*1/7/1/2*1/14...
1 - Сочинение-рассуждение на тему зачем нужна новогодняя елка...
3 - Прочитайте текст.какова его основная мысль ? найдите пять слов,в которых звуковой...
2 - Автобус уехал с остановки в 8ч 56 мин. сколько времени ему потребовалось чтобы...
2 - Почему в 18 веке жизнь людей была столь коротка...
1 - Подбери к пословицам разных народов пословицы с тем же смыслом. 1. тот не заблудиться,кто...
1 - Представьте число в стандартном виде 892140000; 0,004507; 32145,25...
1 - Разложите на простые множители на число: 27; 56; 625; 820; 2772; 702; 1224....
1 - Придмет рассказать про дедушке окружающий мир 3 класс...
3 - По окружающему миру 3клаас обозначь на схеме основные и промежуточные стороны...
2
Дробь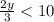 и
и 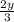 ∈
∈ 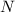
1)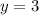 =>
=> 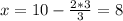
2)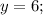 =>
=> 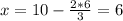
3)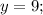 =>
=> 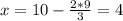
4)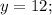 =>
=> 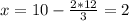
5)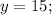 =>
=> 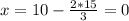
Число 0 не является натуральным числом, поэтому пара (0; 15) не является решением рівняння 3x + 2y = 30.
Все пары: (8; 3), (6; 6), (4; 9), (2; 12)
Вiдповiдь: 4 пары