Знайдіть, при якому значенні параметра k многочлен x^4-4x^3+kx^2-13x+6 ділиться на многочлен x-2

Question

Алгебра: Знайдіть, при якому значенні параметра k многочлен x^4-4x^3+kx^2-13x+6 ділиться на многочлен x-2

lerka157 · Answer

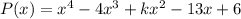Многочлен P(x)=x^4-4x^3+kx^2-13x+6 делится на (x-2) , если остаток от деления P(x) на (x-2) равен нулю.

x - 2 = 0 откуда x = 2 - корень многочлена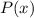 P(x) . Подставив этот корень в многочлен четвертой степени, получим

$P(2)=2^4-4\cdot 2^3+k\cdot 2^2-13\cdot 2+6=4k-36$ - остаток от деления многочлена P(x) на (x-2) и должен он равняться нулю

$4k - 36 = 0\\ 4k=36\\ k=9$

ответ: при k = 9.