Знайдіть похідну функції f , якщо
Другие вопросы по теме Алгебра
Популярные вопросы
- В73 г соляной кислоты с массовой долей 5% поместили избыток цинка. вычислите...
3 - Синтаксический разбор предложения. песни жаворонков снова зазвенел в...
1 - Масою 50г з масовою часткою натрій карбонату 0,02...
3 - Составить текст про физкультуру с вводными словами вероятно во-первых...
1 - 40 ! . пример натурального числа, большего на 15, которое делится на...
2 - Впрямоугольном треугольнике abc (угол c=90 градусов)биссектрисы cd и...
3 - Над каждым словом напишите, какой частью речи оно является. запишите,...
2 - Указать подежи у существительных жаворонки взлетали в воздух с радостной...
2 - Нужен доклад по теме: россия-родина моя! ! только не презентация....
3 - Собъяснением,периметр равнобедренного треугольника =37см,а основание...
3
f(x) = tg(π/6 - x/2)
f ` (x) = (tg(π/6 - x/2)) ` = 1/(cos^2(π/6 - x/2)) × (π/6 - 1/2x) ` = 1/(cos^2(π/6-x/2)) × (-1/2) = - 1/2/(cos^2(π/6-x/2))
Производная сложной функции тангенс: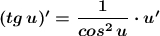 .
.