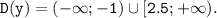Знайдіть область визначення функції: y=√ 2x-5/x+1
Другие вопросы по теме Алгебра
Популярные вопросы
- Гуманные отношения прежде всего связаны с возможностью...
1 - Заполните пропуски в тексте, выбрав слова из предложенного списка. Обратите...
1 - Основными источниками понимания окружающего мира на ранней стадии догосударственного...
2 - Первым источником философской мудрости в Древней Индии стали...
1 - Какое из приведённых высказываний иллюстрирует принцип гуманизма? 1) Любите...
3 - Укажите позицию из перечисленных ниже, которая обобщает приведенный перечень:...
3 - Закончите предложение правильно. Гуманизм — это система воззрений, которая...
3 - Заполните пропуски в тексте, выбрав слова из предложенного списка. Обратите...
1 - Отождествление общества и государства характерно для...
2 - Понятие «даосизм» переводится как...
2
Функция существует, когда подкоренное выражение неотрицательно и знаменатель дроби не равен нулю
Область определения функции: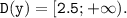
Если же по условию под корнем вся дробь, то решение следующее
Функция существует, когда подкоренное выражение неотрицательно.
ОДЗ: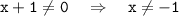
___+___(-1)____-___[2.5]____+__
Область определения функции: