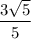Знайдіть найменшу відстань між графіками функцій y=x^2 і y=2x-4
Другие вопросы по теме Алгебра
Популярные вопросы
- M^2-mn-2m+2n если m=0,35, n=0,25 ...
2 - Решить систему методом алгебраического сложения...
2 - С какого года начался постоянный рост температуры на планете? Мой ответ...
3 - Знайдіть точки екстремуму функції y=2x(6)-6x(2)...
2 - 1.Как звали опричника? 2.О чём он печалился на Царском пиру? 3.кому опричник...
3 - Вычислить определённые интегралы методом замены переменной и методом интегрирования...
1 - 105. Орфографический и пунктуационный практикум. Дымковская игрушка представляет...
3 - В якому середовищі діють ферменти ротової порожнини ...
3 - Укажіть число протонів у ядрі елемента, атом якого має на 3 е- більше, ніж його...
1 - Рассчитать таблицу стоимости проездов по городах Украины. В Excel. Прикрепите...
3
Пусть функция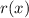 это расстояние между параболой
это расстояние между параболой 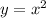 и
и 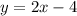 . За аргумент этой функции принимаем абсциссу точки
. За аргумент этой функции принимаем абсциссу точки 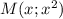 , которая принадлежит параболе.
, которая принадлежит параболе.
Расстояние от точки М до прямой y = 2x - 4 или 2x - y - 4 = 0
откуда x = 1 - критическая точка.
Проверим выполнение достаточного условия экстремума
В частности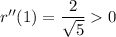 . Следовательно, функция r(x) достигает минимума в точке x = 1/2:
. Следовательно, функция r(x) достигает минимума в точке x = 1/2:
ответ: