Знайдіть екстремальні значення функції y = 1\3 x^3 - 3x^2+20.5
Другие вопросы по теме Алгебра
Популярные вопросы
- Сделать пересказ february 6th 2018. elon musk launches the worlds most powerful...
1 - При яких значеннях b має від єдиний корінь рівняння 3х-4=2b...
3 - Расположить в хронологическом порядке следующие события. укажите ответ в виде...
3 - Велосипедист начинает разгон , имея скорость 10 м/с. если его ускорение равно...
3 - Почему бунин забывает на последних страницах о жене и дочери господина из сан-франциско?...
3 - Какое из чисел 23, 63, 83 является составным? разложите его на простые множители...
3 - Внимательно изучите материал о видах аварий на и взрывоопасных объектах и укажите...
2 - 1найти площадь квадрата со стороной 5см 2 найти площадь прямоугольника стороны...
2 - 10 любителей подледного лова рыбы независимо друг от другапроизвольным образом...
3 - Россия многонациональное государство в 15 веке...
1
y(0) = 20,5
y(6) =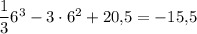
ответ: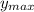 = 20,5;
= 20,5; 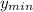 = -15,5.
= -15,5.