Зная, что ряд , найти сумма ряда, полученного путем перестановки его членов
[tex]1+\frac{1}{3} -\frac{1}{2}+\frac{1}{5} +\frac{1}{7} -\frac{1}{4}+/tex]

Пример

Последовательность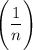 монотонно стремится к нулю, поэтому по признаку Лейбница ряд сходится. Найдем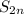

Выпишу формулу Эйлера)))) Пусть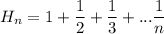 . Эйлер получил асимптотическое выражение для суммы первых n членов ряда:

где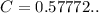 - постоянная Эйлера, при 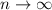значение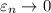

Следовательно,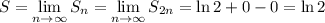

- последовательность частичных сумм данного ряда.

Это мы показали что тот ряд равен ln 2. Теперь перейдем к нашем заданию.

В силу примера, что мы показали в начале, мы получим

Первые две скобки - ряда сходятся, теперь нужно показать что последнее тоже сходится. Рассмотрим ряд

Пусть a > b, тогда

Тут (Sn) - последовательность частичных сумм исследуемого ряда.

Прибавляя и вычитая в выражение слагаемое, мы получим

По формуле Эйлера

Переходя к пределу при n стремящихся к бесконечности, мы получим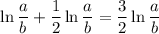

Для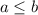 аналогичным образом получается тот же результат. В частности если a = 2, b = 1, получим