Знатоки, не могли бы вы с производными?
Найдите 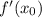 когда:
когда:
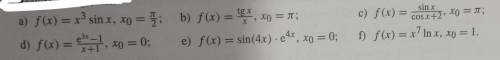
Другие вопросы по теме Алгебра
Популярные вопросы
- Объясните тему.воздух-смесь газов (компоненты,и что это значит) благородные...
2 - Саша задумал число затем разделил 54 на задуманное число прибавил к результату...
2 - Найдите отношение сопротивления двух медный проводников, если длина и...
2 - Два рубля рублями, рубль-пятаками три копейки-по копейке рубль и пяток....
2 - принять решение как заменить одним словом...
1 - Действие уксусной кислоты на оксид кальция. уравнение...
3 - Доля населения занятого в сфере услуг от общего числа занятых в хозяйстве...
2 - На брусок массой 500г, лежащий на шероховатом столе, начали действовать...
2 - Действие уксусной кислоты на оксид кальция. уравнение...
2 - Сколько слов в предложении ? миша и петя были в парке....
2
Наслаждайся)
Объяснение:
a)
b)
c)
d)
e)
f)