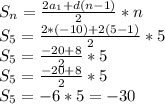Желательно с решением. 1){bn} - прогрессия. найдите b6, если b1=4, q=одна вторая. 2)найдите сумму бесконечной прогрессии: 12; 6; 3)найдите сумму ста первых членов последовательности {xn}, если xn=2n+1 4) {bn} - прогрессия, b1=625, q=одна пятая. найдите s5. 5) арифметическая прогрессия: 10; 8; найдите s10 6) найдите 25-ый член арифметической прогрессии: -3; -6; ; 7) вычислите s4, если {bn} - прогрессия, b1 = 1, q = 3. 8) найдите 8-й член прогрессии (bn), если b1=32, q= одна вторая. 9) {an} - арифметическая прогрессия и a1= -10, d=2. найдите s5.
Другие вопросы по теме Алгебра
Популярные вопросы
- Что обозначают эти знаки?и в какой вид знаков это относится ?...
1 - Отрезок АМ- биссектриса равнобедренного треугольника АВС и основанием АС. Через...
2 - Алдаркөсе мен ұры мултьфильмин естеріңе түсіріңдер.Берілген суреттер бойынша əңгімелеп...
3 - Власне висловлювання на тему: Мовна особистість в українській літературі,та історії...
1 - Який об’єм сульфур(ІV) оксиду вступить в реакцію з 18 г води з утворенням сульфітної...
1 - Решите Найдите девятый член арифметической прогрессии, у которой член равен -65,...
1 - Кто и как впервые осуществил передачу электромагнитного сигнала на расстоянии? ...
2 - Значение птиц для природы и в жизни человека?...
3 - Сергей потратил в интернет-магазине 2320 руб. На покупку флеш-карты он израсходовал...
3 - Розв яжіть рівняння sinx+√3cosx=1...
1
1)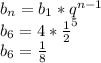
2)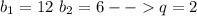
3)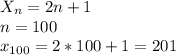
4)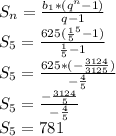
5)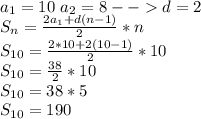
6)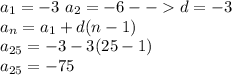
7)
8)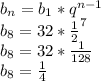
9)