Здравствуйте решить систему уравнений: 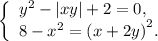
Заранее
Другие вопросы по теме Алгебра
Популярные вопросы
- Для проведения эксперимента предложены следующие реактивы s+hno3 = h2so4 + no2...
3 - Температура воздуха на вершине горы в точке, обозначенной на рисунке буквой а,...
2 - Положительные и отрицательные события социальной сферы во времена великой отечественной...
3 - Выберите правильный союз: 1. robert koch (1843-1910) ist der begründer der modernen...
3 - Сколько значимых в слове подрастёшь?...
1 - Чему равен дискриминант квадратного уравнения 3x-1+6x²=0....
3 - Задайте 4 типа вопросов к следующему предложению in 2008,an australian woman lost...
2 - Даны вещества сu cucl2 naoh h2so4 k3po4 mgo используя их и воду составте оксид...
2 - Люди выдумать ритм для слова eagle...
2 - Найдите угловой коэффициэнт касаткльной к графику функцииf(х)=х2+2х+3 в точке с...
2
Объяснение:
Подставляем х=0 и у=0 в первое уравнение:
y²-|0*0|+2=0
y²+2=0.
Но у²+2>0 ⇒ корни системы х=0 и у=0 - лишние.
Подставляем х=-2√2 и у=√2 в первое и второе уравнение:
Подставляем х=2√2 и у=-√2 в первое и второе уравнение:
ответ: x₁=-2√2 y₁=√2 x₂=2√2 y₂=-√2.